High Precision CKKS Bootstrap: From Discrete CKKS and EvalRound+

September 01, 2025

2025

TL;DR: Recently, a new CKKS bootstrapping paradigm has been suggested, which takes particular advantage of high-precision real/complex-valued computation. In this article, we discuss the recent CKKS bootstrapping technique in CKSS25, utilizing the Discrete CKKS and Grafting from the first two blogposts.

Why High-Precision Bootstrapping Matters

CKKS bootstrapping aims to refresh ciphertexts by increasing their modulus while preserving the encrypted message, enabling further homomorphic computations. However, the bootstrapping introduces approximation error, which causes additional error in the resulting message. Most existing implementations achieve 5–25 bits of precision, where the bit-precision can be defined as the negative base-2 logarithm of the worst-case error, measured across many runs.

Some advanced applications, however, require much smaller error to support stronger security properties such as Circuit Privacy, IND-CPA-D Security, or for Threshold-FHE. These are often achieved via noise flooding—adding exponentially large noise relative to the error before decryption—which screen the secret-related error terms but also the lower bits of the message. It therefore requires significantly higher computational precision, typically 64–80 bits or more.

Supporting such high precision securely and efficiently is a key challenge in CKKS bootstrapping. In LLK+22, a high-accuracy polynomial approximation method for \((x \bmod q)\) operation was introduced, that enables high-precision CKKS bootstrapping but with enormous modulus consumption. In BCC+22, Meta-BTS, the prior state-of-the-art for high-precision CKKS bootstrapping, achieves its precision by performing multiple times the standard low-precision bootstrappings, but at the cost of increased latency linear in the bit-precision with slightly increased modulus consumption.

EvalRound+ Paradigm for High Precision

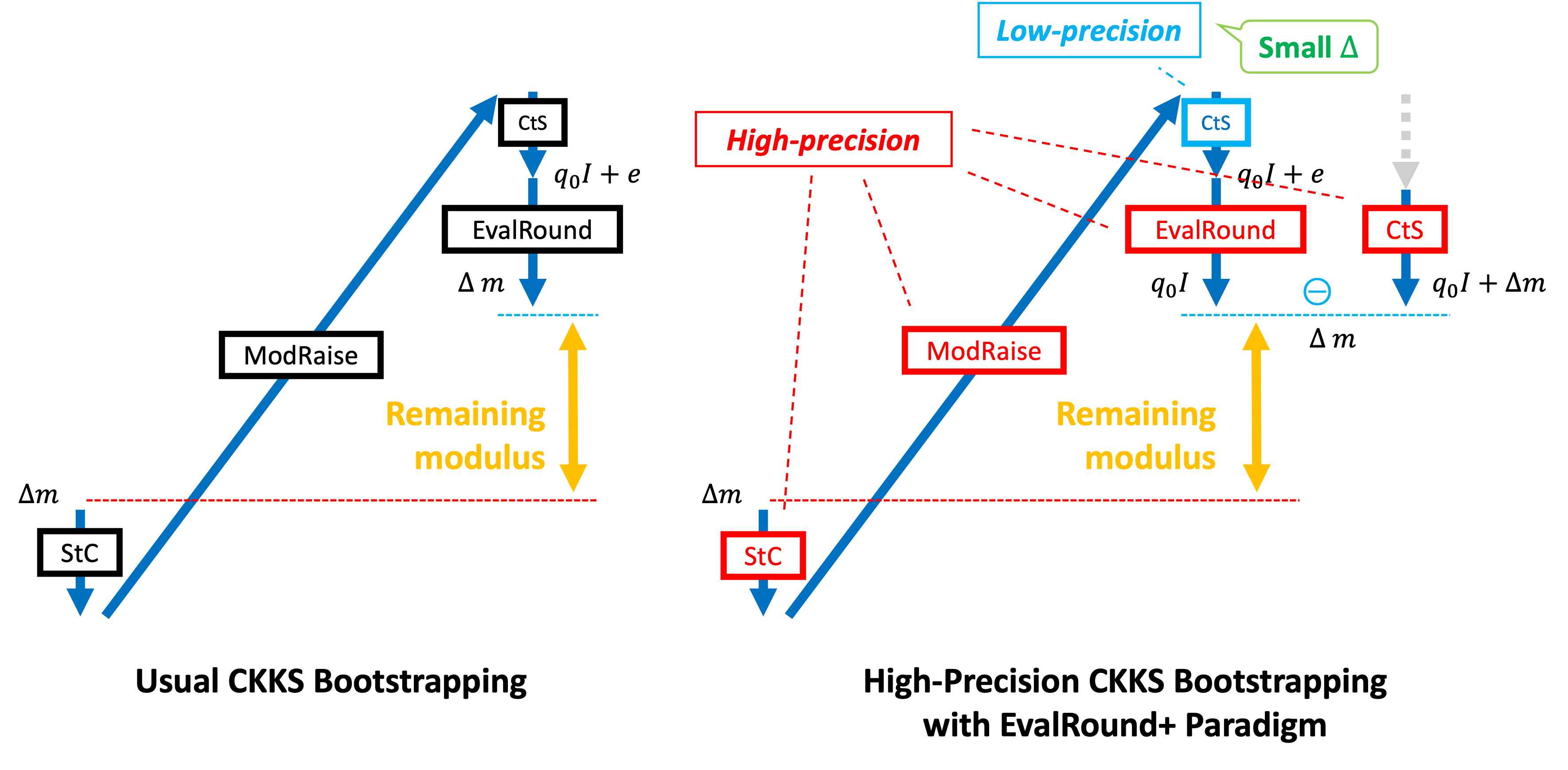
Traditional CKKS bootstrapping follows a pipeline: \(\mathsf{ModRaise} \rightarrow \mathsf{CoeffsToSlots} \rightarrow \mathsf{EvalMod} \rightarrow \mathsf{SlotsToCoeffs}.\) Alternatively, one may place \(\mathsf{SlotsToCoeffs}\) at the beginning, but we focus on the \(\mathsf{ModRaise}\)-first variant, as the technical details remain equivalent.

The EvalRound+ paradigm, introduced in SSKM24, replaces \(\mathsf{EvalMod}\) with a new subroutine called \(\mathsf{EvalRound}\), originally defined in KPK+22 as: \(\mathsf{EvalRound} = \mathsf{Id} - \mathsf{EvalMod}.\) That is, while \(\mathsf{EvalMod}\) extracts the message \(m\) from \(m + q_0 I\), \(\mathsf{EvalRound}\) extracts \(q_0 I\). Note here that the message \(m\) is a plaintext, encoding a complex vector with a complex embedding and a scale factor \(\Delta\).

The EvalRound+ method begins with \(\mathsf{ModRaise}\) and then branches into two parallel tracks:

  • One applies the standard \(\mathsf{CoeffsToSlots}\),
  • The other uses a lower-precision variant \(\mathsf{CoeffsToSlots}^*\) followed by \(\mathsf{EvalRound}\).

Then it subtracts the two resulting ciphertexts, and concludes with \(\mathsf{SlotsToCoeffs}\).

The two branches produce ciphertexts encrypting \(m + q_0 I\) and \(q_0 I\), respectively. Their subtraction yields a ciphertext encrypting \(m\), which is then passed through \(\mathsf{SlotsToCoeffs}\) to return to coefficient representation. Although the dual-track structure increases latency, it reduces modulus consumption, since only the second track dictates the modulus consumption and \(\mathsf{CoeffsToSlots}^*\) require much fewer modulus consumption than the usual \(\mathsf{SlotsToCoeffs}\).

To enable high-precision bootstrapping, we need to upgrade \(\mathsf{CoeffsToSlots}\), \(\mathsf{EvalRound}\), and \(\mathsf{SlotsToCoeffs}\) to their high-precision versions. Each of these operations requires larger scale factors, which in turn increases modulus consumption. Notably, \(\mathsf{CoeffsToSlots}^*\) can remain low-precision and consumes significantly less modulus compared to the others. This marks a key distinction from standard CKKS bootstrapping, where the high-precision \(\mathsf{CoeffsToSlots}\) contributes to overall modulus consumption.

In particular, \(\mathsf{EvalMod}\) and \(\mathsf{EvalRound}\) rely on polynomial approximations of \((x \bmod q)\) and \((x - (x \bmod q))\), respectively. Achieving higher approximation accuracy requires higher-degree polynomials, whose multiplicative depth grows as \(\Theta(\log t)\), where \(t\) is the target bit precision. Combined with scale factors that grow with \(\Theta(t)\), the overall modulus consumption typically scales as \(\Theta(t \log t)\).

Integer Cleaning from Discrete CKKS

Let’s take a closer look at the \(\mathsf{EvalRound}\) procedure. It maps \((I+m/q_0) \mapsto I\), when treating \(q_0\) as a new scale factor, or more precisely, an erroneous integer \(I + \varepsilon\) is maped into a (much less) erroneous integer \(I + \varepsilon'\) where \(\varepsilon = m/q_0 \gg \varepsilon'\). As it cleans a noisy integer, hence we call this functionality as Integer Cleaning. In CKSS25, a novel effectivve high-precision integer cleaning algorithm is introduced based on this interpretation. The process involves:

  1. Digit Extraction: Decompose the noisy integer \(I+\varepsilon\) into base-\(\beta\) digits: for \(I = \sum_{i=0}^{\ell} I_i \beta^i\), each erroneous digit \(I_i + \varepsilon_i\) extracted and stored separately. This can be done by using one among:
    • Direct polynomial approximations for digit extraction, mapping \(I \in [-K, K] \mapsto I_i \in [0, \beta)\), or
    • Mapping \(I\) into \(\exp(2i\pi I / \beta^\gamma)\), the complex \(\beta^\gamma\)-th roots of unity (as in CKKL24) and decomposing the digits via interpolation (as in BKSS24).
  2. Iterative Digit Cleaning: Apply low-degree polynomials iteratively to each noisy digit in order to refine its precision. Each iteration can double the digit’s bit-precision using, for example:
    • For \(\beta = 2\), use \(h_1(x) = 3x^2 - 2x^3\) from CKK20.
    • for \(\beta = 3\), use \(\frac{1}{3}(\bar{x}^2 + 4x - 2x^2\bar{x})\) from BKSS24.

    These polynomials quadratically clean the bit and trit, respectively, refining a \(t\)-bit precision into around \(2t\)-bit precision, yielding a cleaned digit \(I_i + \varepsilon'_i\) with \(\varepsilon'_i \ll \varepsilon_i\) for each \(i\). Note that for each iteration, the scale factor should be large enough to handle the precision of the cleaned digit, roughly squared after each iteration. This implies that the scale factors for the early iterations (as well as the Digit Extraction) can be much smaller (e.g., 25–35 bits) than the desired integer cleaning precision.

  3. Recombination: Combine the cleaned digits \(I_i + \varepsilon'_i\) to reconstruct the high-precision integer \(I + \varepsilon'\). This can be done via integer multiplications and additions, with no modulus consumption.

If the input erroneous integer \(I + \varepsilon\) is \(t\)-bit precise (i.e., \(|\varepsilon|_\infty \leq 2^{-t}\)), then after Integer Cleaning with \(\mathsf{iter}\) iterations of Iterative Digit Cleaning, the output achieves a precision of approximately \(\Theta(2^{\mathsf{iter}} \cdot t)\) bits.

Thrifty Approach for Digit Cleaning

We now require the last piece for making our high-precision bootstrapping more modulus-efficient, by saving modulus for each Digit Cleaning operations.

For a scale factor \(\Delta\) of an input ciphertext, usual homomorphic polynomial evaluation ends up with the same scale factor \(\Delta\) when the maximum bit-precision of the homomorphic polynomial evaluation is \(\mathcal{O}(\log \Delta)\). This means that each Digit Cleaning should use a scale factor \(\Delta = \Omega(2^{2t})\) for the inputs’s bit-precision \(t\), and thus the homomorphic polynomial evaluation for the degree-\(3\) polynomial \(h_1\) will consume \(\lceil \log_2 3 \rceil \cdot \log_2 \Delta \approx 4t\) bits of modulus. That is, for the last iteration of Iterative Digit Cleaning, one needs around \(80\)-bit scale factor and consumes \(160\) bits of modulus, which is a lot.

We therefore suggest a cute but effective Thrifty Approach, which consumes only half compared to the usual approaches, via lazy relineraization and rescale:

  1. For \(\mathsf{ct}_1 = \mathsf{Enc}_{s}(\Delta x)\) in modulus \(Q\), we tensor it into \(\mathsf{ct}_2 := \mathsf{ct}_1 \otimes \mathsf{ct}_1 = \mathsf{Enc}_{s^2}(\Delta^2 x^2)\), where \(x\) is the erroneous bit and \(\Delta\) is an integer scale factor.
  2. We then tensor it again into \(\mathsf{ct}_3 := \mathsf{ct}_1 \otimes \mathsf{ct}_2 = \mathsf{Enc}_{s^3}(\Delta^3 x^3)\).
  3. Multiply the integer \(3\Delta\) and \(2\) to \(\mathsf{ct}_2\) and \(\mathsf{ct}_3\), respectively, and subtract them leads to \(\mathsf{ct}_4 = \mathsf{Enc}_{s^3}(\Delta^3 (3x^2 - 2x^3)) = \mathsf{Enc}_{s^3}(\Delta^3 \cdot h_1(x))\).
  4. Relinearize \(\mathsf{ct}_4\) into \(\mathsf{ct}_4 = \mathsf{Enc}_{s}(\Delta^3 \cdot h_1(x) + e_\mathsf{KS})\), via key-switching keys for \(s^3 \rightarrow s\) and \(s^2 \rightarrow s\), where \(e_\mathsf{KS}\) is the key-switching error.
  5. Finally, rescale by \(\Delta\), resulting in \(\mathsf{ct} = \mathsf{Enc}_{s}(\Delta^2 \cdot h_1(x) + e)\) in modulus \(Q/\Delta^2\). Here, the error can be written as \(e = \lceil e_\mathsf{KS}/\Delta^2 \rfloor + e_\mathsf{RS}\) with the rescale error \(e_\mathsf{RS}\), which in turns \(e = \mathcal{O}(1)\).

This allows one to use \(\Delta = \Theta(2^t)\) for the input ciphertexts and to consume \(\approx 2t\) bits of modulus, which results in about twice the input precision:

\[\left| (h_1(x) + e / \Delta^2) - \lceil x \rfloor \right| \le |h_1(x) - \lceil x \rfloor| + |e / \Delta^2| = \mathcal{O}(2^{-2t}),\]

since, given \(\left| x - \lceil x \rfloor \right| \le 2^{-t}\), it follows that \(\left| h_1(x) - \lceil x \rfloor \right| = \mathcal{O}(2^{-2t})\).

Note that the approach naturally extends to other types cleaning polynomials with similar impact on the modulus consumption.

All Together

The new CKKS bootstrapping system proposed in CKSS25 is built upon the following building blocks:

  • EvalRound+ paradigm as the structural backbone,
  • High-precision Integer Cleaning based on Discrete CKKS,
  • Thrifty Approach for evaluating the cleaning polynomials with reduced modulus,
  • Grafting technique from CCK+24 for efficient computation with a lot of small scale factors.

When the high-precision Integer Cleaning is incorporated into the EvalRound+ paradigm, the small scale factors can also be used during \(\mathsf{CoeffsToSlots}^*\), which makes the overall bootstrapping procedure highly efficient in terms of modulus consumption. Those small scale factors lead to many small RNS factors, potentially degrading performance, which is exactly where Grafting excels.

In a proof-of-concept implementation with ring dimension \(N = 2^{16}\), the bootstrapping was tested across the four variants — using either bits (\(\beta=2\)) or trits (\(\beta=3\)), and two digit extraction strategies (direct approximation vs. through roots-of-unities). The result: up to 81-bit precision in a full-slot bootstrapping, with 1.64× speedup over Meta-BTS (which achieves similar accuracy through four sequential bootstraps). Moreover, the new bootstrapping came with slightly reduced modulus consumption, leaving 494 bits available for non-bootstrapping computations.

Thanks to its iterative cleaning nature, it naturally scales further. While our implementation uses libquadmath for the CKKS encoding and decoding, higher precisions can also be supported using multiple-precision data types, for e.g., one extra cleaning iteration will lead to around 150-bit precision at \(N = 2^{16}\) with a slightly larger latency, while preserving at least one level for homomorphic multiplication (with a modest increase in scale factors for \(\mathsf{CoeffsToSlots}\) and \(\mathsf{SlotsToCoeffs}\), but not for \(\mathsf{CoeffsToSlots}^*\)).