Convergent Evolution: Why Secure Homomorphic Encryption Will Resemble High-Performance GPU Computing

• Written by Sunchul Jung (CryptoLab)

TL;DR: Fully Homomorphic Encryption (FHE) programming hits a fundamental Turing Barrier where secure computation forbids the dynamic branching that makes conventional software work, forcing it into a parallel-first paradigm surprisingly similar to the high-performance GPU model. This means the future of FHE isn’t a magic compiler, but a hybrid architecture where a trusted client orchestrates complex logic, while an untrusted server executes simple, branchless secure kernels on encrypted data across a well-defined offloading boundary. Ultimately, developers must stop trying to translate old optimization habits and start redefining problems from the ground up, because in the world of FHE, performance isn’t about pruning—it’s about parallelism.

---

Abstract

Fully Homomorphic Encryption (FHE) and high-performance GPU computing have evolved under fundamentally different pressures—security and performance—yet I argue that their programming models are converging toward a branch-free, massively parallel paradigm.

This convergence arises from FHE’s Turing Barrier: while FHE is theoretically Turing-complete at the gate level, supporting secret-dependent control flow securely is practically infeasible without incurring combinatorial overheads. Meanwhile, GPUs evolved under different constraints—avoiding warp divergence—but reached similar design instincts: uniform, parallel-first kernels.

However, FHE introduces strictly stronger constraints than GPUs:

• Every kernel must be data-oblivious.
• Memory access patterns must remain uniform.
• The Host ↔ Device (Trusted-Host ↔ Secure-Kernel-Executor in the FHE context) offloading boundary must be formally defined.

Using Quicksort and Approximate Nearest Neighbor (ANN) search as case studies, I show why pruning-based optimizations—highly effective in plaintext—become anti-secure (i.e., the act of optimization itself introduces security vulnerabilities contrary to the original intention) under encryption. Recent works, including the FHE compiler project HEIR¹, programmable bootstrapping optimizations², and private inference frameworks³, confirm these fundamental constraints, demonstrating incremental improvements within fixed sandboxes but falling short of general solutions.

I conclude that the future of practical FHE lies in hybrid architectures where trusted clients orchestrate control flow and untrusted servers execute branchless, parallel secure kernels. GPU programming models provide valuable blueprints, but advancing secure computation demands an FHE-native programming model.

---

Table of Contents

1. Introduction
2. Background: Fundamental Constraints
   2.1. The FHE Security Model and the Turing Barrier
   2.2. How FHE Compilers Handle Control Flow
   2.3. Compilation Resource Explosion Warning
   2.4. Programmable Bootstrapping and Its Limits
   2.5. Memory Access and ORAM Lower Bounds
3. Convergent Evolution: FHE and GPUs
4. A Practical Architecture: The Hybrid Model
5. Case Studies: The Parallel-First Imperative
6. Comparative Analysis of Recent Research
7. Implications for FHE Systems
8. Conclusion: The Path to FHE-Native Development
9. References

---

1. Introduction

Fully Homomorphic Encryption (FHE) enables arbitrary computation on encrypted data without exposing plaintexts⁴. Meanwhile, GPUs have revolutionized computing by enabling massive parallelism, powering deep learning and high-performance computing⁵.

Despite different origins, these two paradigms now face structurally similar challenges. The need for a parallel-first model in FHE arises from a dual mandate:

• Security: Translating secret-dependent branching from conventional programs introduces critical side-channel leakage risks, forcing a branchless, data-oblivious model.
• Performance: FHE operations are often heavily memory-bound, and mitigating the I/O overhead caused by chaining multiple operations requires exploiting massive parallelism via fused, coarse-grained kernels.

This blog explores why these dual pressures lead to a convergence with the GPU model, why traditional optimizations fail, and why the future depends on building a new ecosystem of FHE-native, fused kernels managed by a smart, hybrid architecture.

2. Background: Fundamental Constraints

2.1 The FHE Security Model and the Turing Barrier

An FHE scheme evaluates $f(\mathrm{Enc}(x)) \rightarrow \mathrm{Enc}(f(x))$ without revealing $x$. However, secure execution forbids revealing control flow or memory access patterns derived from secret data.

Dynamic branches and loops are problematic:

• if-else decisions → leak branch outcomes.
• Secret-dependent loops → leak iteration counts.

Thus, FHE programs must adopt data-oblivious execution⁶:

• Evaluate both paths of all branches.
• Fix loop bounds to public constants.
• Make memory accesses uniform.

This reality is summarized as the Turing Barrier: FHE remains Turing-complete in theory at the gate level, but we use this term to describe the practical infeasibility of securely compiling general-purpose programs that rely on unrestricted control flow.

2.2 How FHE Compilers Handle Control Flow

Many developers assume FHE behaves like a traditional runtime: write an if statement, and only the chosen branch executes. But this would leak secrets—if the server observes which path was taken, it learns private data.

In FHE, both branches must always execute. The compiler produces an arithmetic select: \(\mathrm{Enc}(r) = \mathrm{Enc}(\text{cond}) \cdot \mathrm{Enc}(r_a) + (1 - \mathrm{Enc}(\text{cond})) \cdot \mathrm{Enc}(r_b)\)

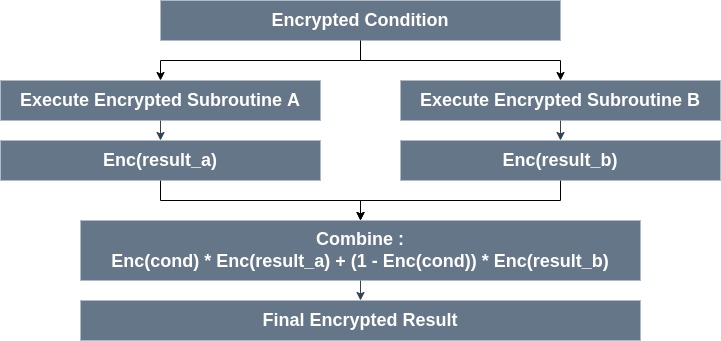
Key takeaway: Under FHE, writing if (encrypted(cond)) ... in source code does not imply conditional execution; the compiler always executes both paths and combines results securely.

2.3 Compilation Resource Explosion Warning

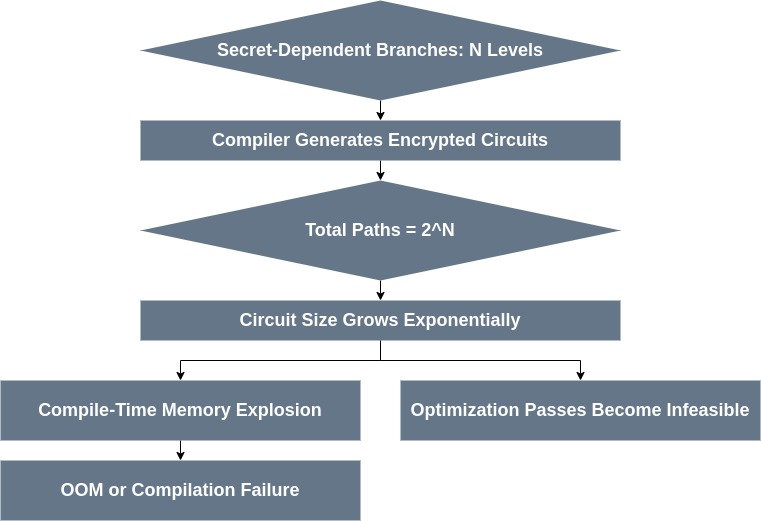
The combinatorial blow-up caused by encrypted control flow affects not only runtime performance but also the compilation process itself. For every secret-dependent branch, the FHE-aware compiler must materialize all possible subroutines into encrypted circuits. In the worst case, $N$ nested conditions yield a circuit size of $O(2^N)$.

Recent experiments with LLVM-based FHE Intermediate Representations (IRs) such as HEIR ¹ highlight this challange. While research explores sophisticated optimizations to avoid naive full unrolling (e.g., by hoisting common code from both branches), these techniques can only mitigate the overhead for shared computational paths. For genuinely divergent logic, the compiler must still materialize a circuit whose complexity grows exponentially with the number of secret-dependent branches.

It is therefore an expected and observable outcome that beyond a certain branching complexity, this exponential growth will cause the compiler to exhaust system resources, leading to out-of-memory (OOM) errors—before execution even begins. This demonstrates that directly translating branch-heavy business logic is infeasible. Problem redefinition is not an optimization choice — it is a requirement for tractable FHE compilation.

2.4 Programmable Bootstrapping and Its Limits

TFHE’s Programmable Bootstrapping (PBS)⁷ and CKKS’s BB-BTS (Batch-bits Bootstrapping)⁸ enable efficient Look-Up Table (LUT)-based evaluation of small non-linear functions. Recent works on optimizing these circuits² further reduce cost by compressing LUT evaluation.

However, PBS does not eliminate the combinatorial blow-up of complex business logic:

• Optimizations are pattern-limited, applicable to fixed, low-dimensional functions.
• Decision-tree inference using private inference frameworks like Piranha³ works only for small, fixed-depth trees; adaptive branching remains insecure.

PBS provides a valuable tool but not a universal escape hatch.

2.5 Memory Access and ORAM Lower Bounds

Just as control flow must be made data-oblivious, memory access patterns must also be protected. When computations require secret-dependent memory access, Oblivious RAM (ORAM) must be used to hide patterns⁶. However:

• ORAM has a provable lower bound: $\Omega(\log n)$ per access, where n is the number of blocks in memory.
• Even optimal constructions like OptORAMa⁹ cannot break this limit.
• For large-scale workloads, ORAM costs dominate if memory access depends on secrets.

Implication: Secret-driven memory access cannot be made “cheap” under FHE. Algorithms must be redesigned to avoid adaptive memory patterns.

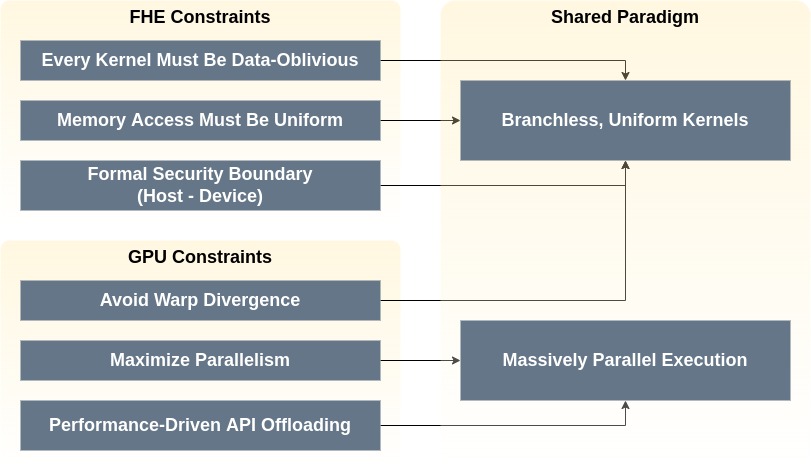
3. Convergent Evolution: FHE and GPUs

FHE and GPU computing converge structurally, driven by the dual pressures of security and performance.

Aspect	GPU Offloading (CUDA/ROCm/SYCL)	FHE Hybrid Model (Proposed)
Primary Goal	Maximize throughput	Preserve confidentiality
Execution Style	SIMT (Single Instruction, Multiple Threads), branch-minimized	Branchless, data-oblivious
Offloading Model	Implicit, library-driven	Explicit, security-driven
Boundary Definition	Kernel APIs, runtime libraries	Formally defined security surface
Workload Assumption	Dense, GPU-friendly ops	Arbitrary → refactoring needed
Memory Model	Observable, hierarchical	Must be oblivious
Programming Model	Emergent, pragmatic	Intentional, security-first

FHE’s constraints are stricter, mandating a more intentional and formally defined programming model than the emergent, pragmatic model of GPUs. We must explicitly define host-device offloading and design kernels intentionally.

4. A Practical Architecture: The Hybrid Model

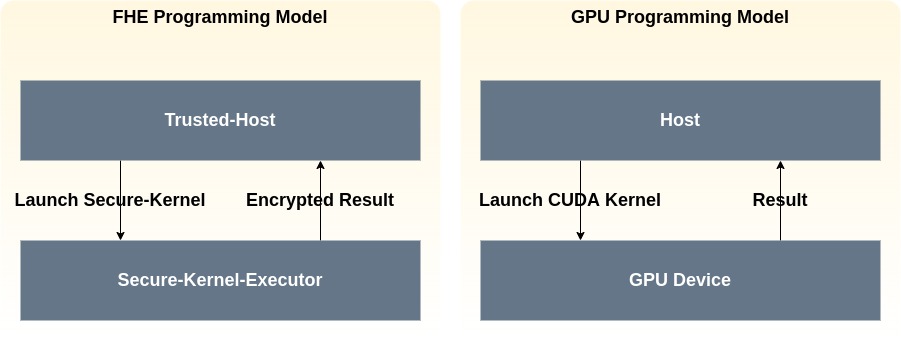
Terminology Note: I borrow the host-device terminology from GPU programming models for intuitive consistency. In the FHE context:

• Host → Trusted-Host: Orchestrates application logic, manages secret-dependent control flow, and launches secure kernels.
• Device → Secure-Kernel-Executor: Executes branchless, data-oblivious kernels on encrypted inputs in an untrusted environment.

4.1 Note on GPU Programming Models

Although I borrow GPU programming terminology, GPU programming models themselves are not fully standardized. Offloading is often API-driven via libraries like cuBLAS or TensorRT, not formal control-flow abstractions. This implies an even greater challenge for FHE: we must explicitly define the offloading boundary, because FHE imposes far stricter constraints than GPUs.

5. Case Studies: The Parallel-First Imperative

Developers often misconceive that FHE’s Turing completeness at the gate level implies pruning-based optimizations can be directly ported. However, pruning is anti-secure.

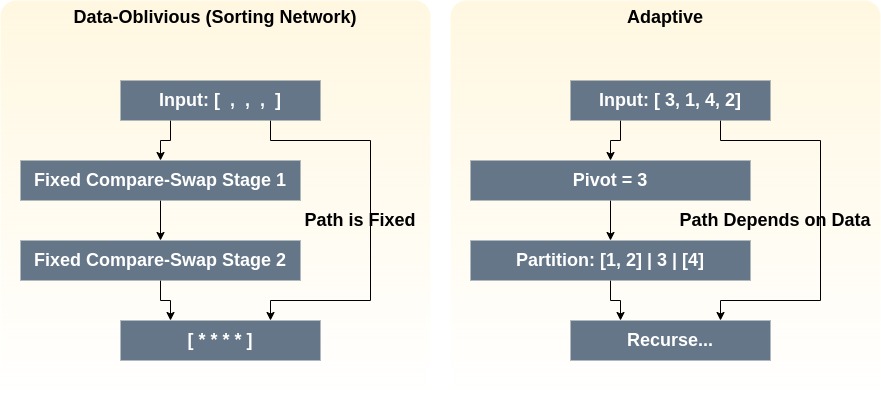
5.1 Sorting

• Quicksort (FHE-unfriendly): Adaptive pivots and partitions leak structural information.
• Sorting Networks (FHE-Friendly): Fixed compare-swap sequences (e.g., Bitonic Sort) are uniform, oblivious, and parallelizable.

5.2 Approximate Nearest Neighbor (ANN)

In this context, N represents the total number of vectors in the dataset, d is the dimension of each vector, k is the number of clusters in the IVF index, and n_probe is the number of clusters to probe during a search.

• IVF-FLAT (FHE-unfriendly): This popular method works by first selecting a few (n_probe) cluster centroids nearest to the query, then searching only within those clusters. This adaptive probing leaks which clusters the query is close to.
• HNSW (FHE-unfriendly): Adaptive graph traversal leaks query-specific paths¹⁰.
• Brute-Force Scan (FHE-Compatible): Evaluate distances for all vectors uniformly.

Algorithm	Plain Complexity	FHE-Compatible Complexity	Overhead Source
IVF-FLAT	$O(k\cdot d + \frac{n_{\text{probe}}}{k}\cdot N\cdot d)$	$O(k\cdot d + N\cdot d)$	Removing adaptive probing
HNSW	$O(d \cdot \log N)$	$O(N\cdot d)$	Eliminating path pruning

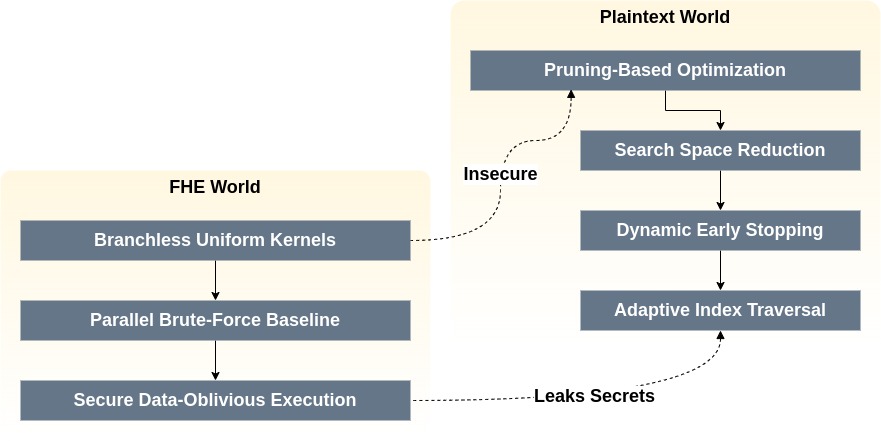
Key Insight: In FHE, brute force is the baseline, not the fallback. Performance gains come from parallelizing fixed workloads, not pruning.

6. Comparative Analysis of Recent Research

Work	Core Idea / Contribution	Scope / Applicability	Limitations & Implications
HEIR1	MLIR-based compiler for FHE	Expressive across CKKS, BFV, TFHE backends	Optimizations can reduce overhead for shared paths, but cannot solve the core combinatorial explosion for divergent logic. Confirms Turing Barrier
PBS Optimization2	PBS circuit optimization for TFHE	Efficient for fixed LUT-based non-linearities	Limited to local patterns; cannot eliminate control-flow explosion
Private Inference3	GPU-friendly framework for private inference	Works for fixed-depth, small models	Not scalable to adaptive branching; dynamic paths remain insecure
OptORAMa9	Near-optimal oblivious memory	Provably tight asymptotics	$\Omega(\log n)$ overhead unavoidable; secure random access is inherently expensive

Recent progress expands FHE’s reach but validates the central thesis: general-purpose, efficient, secure FHE requires problem redefinition, not direct translation.

7. Implications for FHE Systems

• FHE-aware compilers must act as policy enforcers, not magicians:
  • Convert branches into predicated arithmetic.
  • Enforce loop unrolling to constant bounds.
  • Optimize SIMD-style ciphertext packing.
• Hardware accelerators for FHE will increasingly resemble GPUs:
  • High-throughput execution cores.
  • On-die NTT engines.
  • High-bandwidth memory for ciphertext batching.
• Design implication: The parallel-first paradigm isn’t just optimal — it’s necessary for secure performance.

8. Conclusion: The Path to FHE-Native Development

The theoretical Turing completeness of Fully Homomorphic Encryption (FHE) may suggest that any software can be privatized with a magical compiler. In reality, secure computation faces a fundamental Turing Barrier: the dynamic, branching-based optimizations that make conventional software efficient become the very conduits that leak secrets under encryption. The future of FHE, therefore, depends not on translating legacy code, but on redefining problems from first principles.

The most pressing challenge is FHE’s dominant performance bottleneck: memory I/O. Optimizing individual operations in isolation is insufficient; for any non-trivial business logic, the cumulative overhead of sequential IR-level kernels quickly makes applications impractical. Inspired by high-performance GPU computing, the solution is to move from fine-grained primitives toward a hierarchy of fused, coarse-grained kernels—reducing data movement, exploiting massive parallelism, and unlocking practical performance.

Building these kernels also solves the ecosystem’s chicken-and-egg problem: useful, coarse-grained kernels must come first to create immediate value, attract developers, and enable sustainable growth. A lightweight orchestration framework can manage this efficiently, where the trusted host performs simple runtime scheduling—dispatching fused kernels when available and falling back to basic ones otherwise. Since scheduling depends only on the public sequence of API calls, it remains inherently secure.

Beyond kernels, the next step is to formalize the offloading boundary between the trusted host and the secure executor. Unlike GPU computing, where offloading is pragmatic and API-driven, FHE’s boundary is a security contract that must be explicit and rigorously defined. Establishing this foundation transforms FHE development from a set of clever hacks into a true engineering discipline.

Ultimately, this leads to a truly FHE-native programming model. Compilers will evolve from magical translators into policy enforcers, guiding developers toward parallel-first problem formulations. By combining optimized fused kernels with explicit host-device boundaries, we can unlock scalable, secure, and high-performance computation—turning FHE from a theoretical promise into a practical reality.

Looking further ahead, inspiration can be drawn from quantum computing, where developers also work within strict constraints, composing algorithms from a limited set of gates while carefully managing entanglement. Similarly, tomorrow’s FHE developers will think less like conventional software engineers and more like quantum algorithm designers—crafting solutions in a fundamentally constrained, parallel-first universe.

Stop translating. Start redefining.

---

9. References