NeuJeans: Fast Private CNN Inference by Fusing Convolutions and Bootstrapping in FHE

• Written by Jaiyoung Park (Seoul National University)
• Based on https://arxiv.org/pdf/2312.04356 (CCS 2024)

TL;DR: NeuJeans introduces a new “Coefficients-in-Slot” (CinS) encoding for CKKS. It rethinks how convolutions are laid out and fuses them with bootstrapping, cutting latency on big models like ResNet running over ImageNet.

---

CKKS relies on the Ring Learning With Errors (RLWE) problem to encrypt messages into a single ciphertext. This ring structure is key to CKKS’s efficiency, as a single homomorphic operation can act on all encrypted values in parallel.

However, the same structure complicates FHE circuit design. Linear algebra in the RLWE format often forces interactions within a ciphertext, which can dominate runtime by requiring many costly rotations¹. Consequently, an FHE program’s profile can differ significantly from its plaintext counterpart. In deep circuits such as neural networks, bootstrapping further amplifies this challenge.

Encodings in CKKS

In CKKS, the data arrangement within a ciphertext’s underlying polynomial is called its encoding. Different encodings are optimized for different types of computations. Choosing the correct ones and switching between them during an algorithm is crucial for overall performance. The two primary encodings are slot encoding and coefficient encoding. Since CKKS bootstrapping naturally involves transforms between these states, a well-designed application can perform computations in whichever encoding is most efficient at the moment.

In slot encoding, a ciphertext holds a vector of complex numbers in distinct “slots”, and all arithmetic operations are performed element-wise. This structure is ideal for operations that can be parallelized easily, such as applying activation functions to every element in a vector or multiplying a diagonalized matrix with a vector. However, data aggregation across slots relies on rotations, which are computationally expensive.

Conversely, in coefficient encoding, message values are placed directly into the coefficients of the ciphertext polynomial. A multiplication in this layout computes a negacyclic convolution. Formally, for vectors $\mathbf{x}, \mathbf{y} \in \mathbb{R}^\ell$, their product is

\[(\mathbf{x} \circledast_\ell \mathbf{y})_k = \sum_{i=0}^{k} x_iy_{k-i}-\sum_{i=k+1}^{\ell-1} x_iy_{\ell+k-i}, \quad 0 \le k < \ell.\]

This is equivalent to a cyclic convolution with a “wrap-around and sign flip”, reflecting the polynomial modulus $X^\ell + 1$. Such convolutions align well with the operations fundamental to neural networks and signal processing. However, the RLWE ring degree $\ell$ (commonly $2^{14}$ or $2^{15}$ for 128-bit security) is much larger than the typical dimensions of images (e.g., $32 \times 32$ or $16 \times 16$). As a result, a single ciphertext implicitly encodes tens or even hundreds of images. This mismatch complicates efficient implementation, since it forces convolutions to occur across all channels simultaneously.

CinS, or Coefficients-in-Slot encoding, is a generalized structure that combines the properties of both slot and coefficient encoding. If the total message vector has size $\ell=m\times n$, CinS encoding treats the vector as $n$ independent sub-vectors (slots), each of length $m$. Operations are then element-wise across the $n$ sub-vectors but convolutional within each of the $m$ elements. This hybrid approach allows for parallel convolutions. When $m=1$, CinS reduces to standard slot encoding, and when $n=1$, it becomes standard coefficient encoding.

Encoding Transformation

Switching between these encodings is essential for building complex applications. The Slot-to-Coefficient (S2C) transform converts a ciphertext from slot encoding to coefficient encoding, while its inverse (C2S) does the reverse. Fundamentally, the S2C transform is a Discrete Fourier Transform (DFT). To perform it efficiently, the large \(\ell \times \ell\) DFT matrix is decomposed into a product of sparse matrices using the Cooley–Tukey Fast Fourier Transform (FFT) algorithm².

The decomposition is applied to the bit-reversed DFT matrix, \(\mathcal{T}_{\ell}\), which simplifies the FFT structure and is defined recursively:

\[\mathcal{T}_\ell = \begin{bmatrix} I_{\ell/2} & D_{\ell/2} \\ I_{\ell/2} & -D_{\ell/2} \end{bmatrix} \cdot \begin{bmatrix} \mathcal{T}_{\ell/2} & \mathbf{0} \\ \mathbf{0} & \mathcal{T}_{\ell/2} \end{bmatrix}\]

Here, $I_{\ell/2}$ is the identity matrix, \(\mathcal{T}_{\ell/2}\) is the smaller bit-reversed DFT matrix, and $D_{\ell/2}$ is a diagonal matrix of complex “twiddle factors.” Applying this recursion $\log_2 \ell$ times decomposes $\mathcal{T}_\ell$ into a product of highly sparse, block-diagonal matrices.

\[\mathcal{T}_\ell = S_{\ell/2}^{(\ell)} \cdot S_{\ell/4}^{(\ell)} \cdots S_1^{(\ell)}\]

Each matrix $S_k^{(\ell)}$ in this product is a sparse, block-diagonal matrix whose structure is derived from the butterfly operations at each stage of the FFT algorithm.

NeuJeans: CinS Encoding and Fused Operations

NeuJeans defines CinS encoding using a partial S2C transform. Instead of applying the full DFT, it applies only the first $\log_2{m}$ stages, leaving the ciphertext in an intermediate state between slot and coefficient encoding. Formally, for a message vector $\mathbf{x}$ and slot encoding $s(\mathbf{x})$, CinS is:

\[\phi(\mathbf{x};m,n) = S_{m/2}^{(\ell)} \cdots S_{1}^{(\ell)}(s(\mathbf{x}))\]

The strength of this encoding lies in its multiplication. The partial DFT places each sub-vector into coefficient form, so multiplying two CinS ciphertexts directly performs the desired operation: the element-wise negacyclic convolution of the sub-vectors. For two message vectors $\mathbf{x}, \mathbf{y}$, we have:

\[\phi(\mathbf{x};m,n) \odot \phi(\mathbf{y};m,n) = \phi(\mathbf{z};m,n)\]

where each sub-vector of the output, $\mathbf{z}_j$, is the negacyclic convolution of the input sub-vectors:

\[\mathbf{z}_j = \mathbf{x}_j \circledast_m \mathbf{y}_j \quad \text{for } j = 0, \dots, n-1\]

This multiplication property allows NeuJeans to map the many 2D convolutions of a CNN layer into a single homomorphic multiplication.

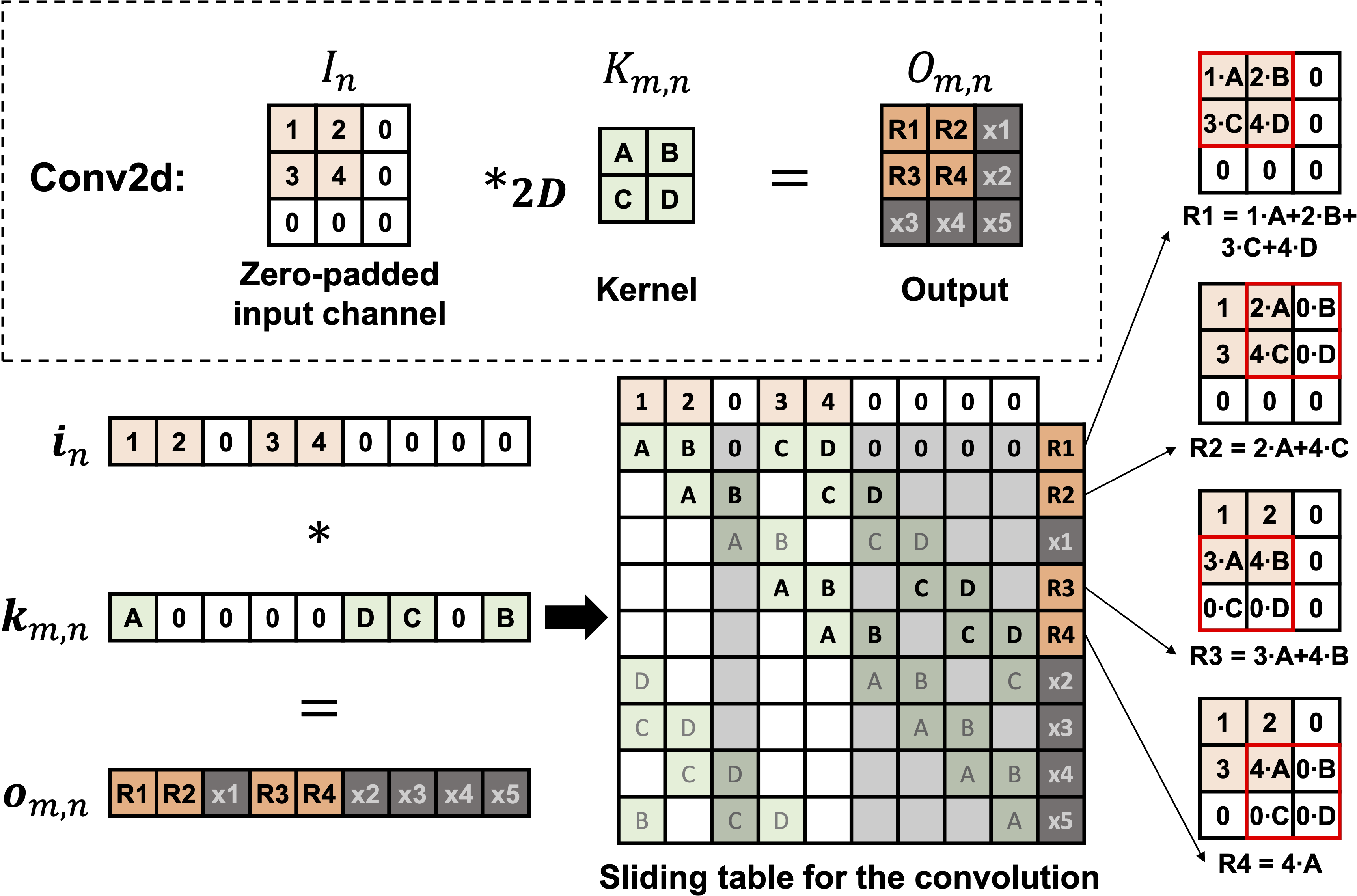
The figure above illustrates this mapping: the image and kernel are zero-padded and flattened, with $I_n$ and $K_{m,n}$ converted into vector $i_n$ and $k_{m,n}$. As shown, the negacyclic convolution $o_{m,n}=i_n \circledast k_{m,n}$ is equivalent to 2D convolution result \(O_{m,n}=O_n*_{2D}K_{m,n}\). The extra terms ($x_1$ to $x_5$) that arise from zero-padding are later removed using a mask vector.

Fusing with Bootstrapping

NeuJeans goes further by fusing the convolution with bootstrapping. Bootstrapping already performs a full S2C transform; NeuJeans inserts the convolution midway, creating a sequence like: [Part 1 of S2C] -> Convolution -> [Part 2 of S2C]

Since both the convolution and the second half of S2C are sparse diagonal matrices, the server can precompute their product offline. At runtime, this reduces to: [Part 1 of S2C] -> [Fused convolution + Part 2 of S2C]

This fusion removes redundant steps, streamlining the bootstrapping process.

Application to Large-Scale CNN Inference

By combining CinS encoding with fused bootstrapping, NeuJeans enables faster 2D convolutions and a leaner S2C transform. We evaluated the approach on ResNet-18/50 and MobileNet-V2 using the HEaaN library. ResNet-18 and ResNet-50 are built primarily from standard convolution layers, whereas MobileNet-V2 adopts depthwise separable convolutions for efficiency.

Across all three models, NeuJeans consistently outperforms prior methods^{3 4} based on slot and coefficient encodings, achieving

• 7.7$\times$-30.3$\times$ speedup in convolution layers
• 1.47$\times$-1.84$\times$ speedup in total inference time

Overall, NeuJeans demonstrates how a small shift in encoding design—using CinS and fusing operations into bootstrapping–can deliver meaningful efficiency gains for encrypted CNN inference. These results underscore encoding design as an effective path for performance optimization. Looking ahead, we aim to extend this approach to emerging architectures, including diffusion models and graph neural networks.