Low Communication Threshold Fully Homomorphic Encryption
- Written by Alain Passelègue
- Based on https://eprint.iacr.org/2024/1984 (Asiacrypt 2024)
TL;DR: We propose a solution based on fully homomorphic encryption for privately delegating computation over data from multiple clients to a trusted server. Our construction ensures that every client’s data remains private to other participants (server and other clients) even if all but one clients collude against the non-colluding client. It is the first to achieve low communication between all parties, as we also prove that prior low communication solutions to this problem are insecure.
Threshold Fully Homomorphic Encryption
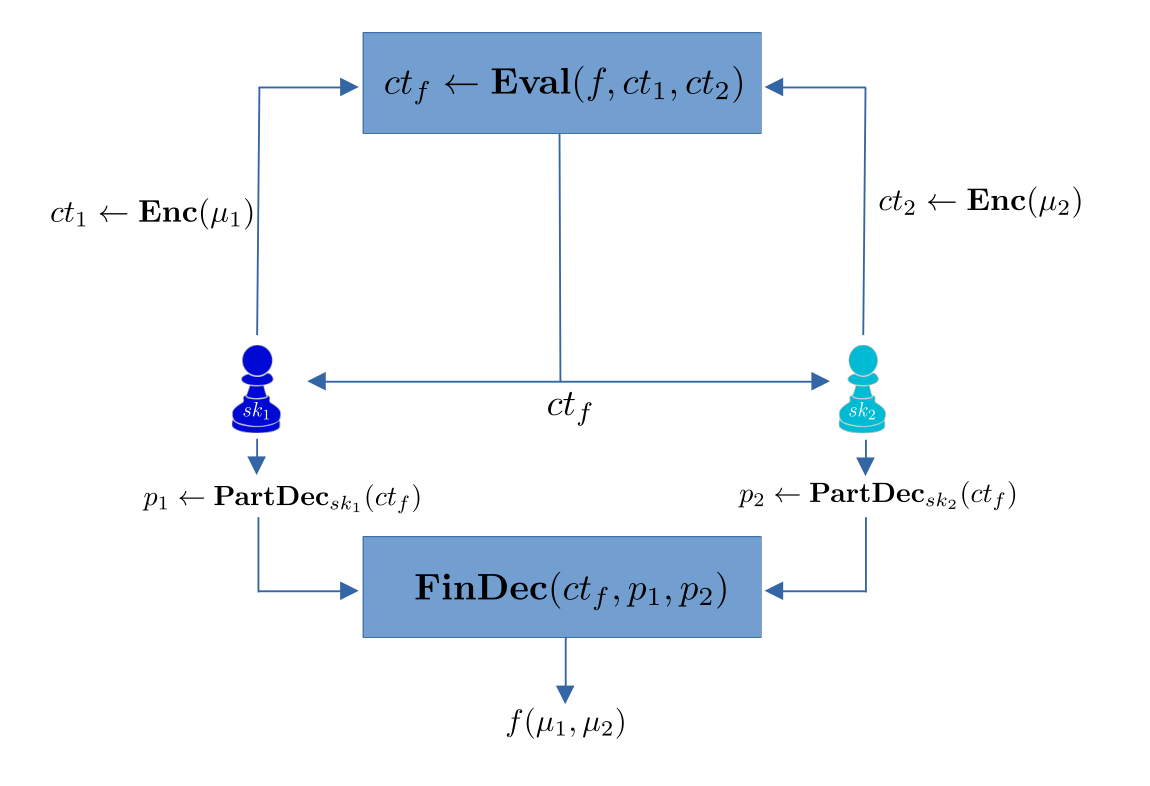
Threshold Fully Homomorphic Encryption (ThFHE) is an extension of Fully Homomorphic Encryption (FHE) in which the decryption key is split between $N$ parties. To decrypt a ciphertext, parties must collaborate. In the $N$-out-of-$N$ setting, which we focus on, all the $N$ parties must take part to decryption in order to be able to decrypt a ciphertext. Moreover, an attacker corrupting all parties but 1 still cannot decrypt. In terms of algorithms, this translates in splitting the decryption algorithm Dec of a standard FHE into two algorithms termed PartDec and FinDec. PartDec allows a party to partially decrypt a ciphertext using its share of the secret key, while FinDec allows to combine the $N$ partial decryptions of a ciphertext obtained from all parties in order to recover the underlying plaintext. Hence, a ThFHE scheme is a tuple (KeyGen, Enc, Eval, PartDec, FinDec), where KeyGen allows to generate the keys, Enc is the encryption algorithm, Eval is the homomorphic evaluation algorithm, and PartDec, FinDec are the two steps of the distributed decryption process.
For example, in the figure below, two parties (blue and teal pawns) respectively encrypt a message $\mu_1,\mu_2$ using Enc. Then, someone (e.g., a party or a server) can use Eval to homomorphically evaluate a function f on the corresponding ciphertexts $ct_1,ct_2$, resulting in a ciphertext $ct_f$. The parties can then collaboratively decrypt to recover $f(\mu_1,\mu_2)$.
ThFHE has numerous applications, as it in particular enables:
- (1) more secure key management by splitting the decryption key accross multiple devices;
- (2) joint computation on private data by having parties encrypting their individual data and decrypting only the result of the homomorphic computation;
- (3) threshold cryptography at large, e.g. threshold signatures.
From FHE to ThFHE
As of today, practical FHE schemes encrypt a plaintext $m$ as a ciphertext of the form $(a,b)$ satisfying $as+b = \Delta \cdot m + e$ for some small error $e$ referred to as the computation error and where $s$ denotes the secret key defined over some modulus $q$. Decrypting $(a,b)$ thus simply consists in computing $as+b$, which is linear in the secret key $s$. Concretely, the quantities $a,s$ are either vectors or polynomials over $Z_q$. For simplicity, we assume they are vectors, and then computing $as$ means computing the inner product between $a$ and $s$.
Such an FHE scheme can then be transformed into a ThFHE scheme by additively sharing the key between the $N$ parties, i.e. by sampling $s_1, …, s_N$ uniformly at random modulo $q$ satisfying $s_1 + … + s_N = s \mod{q}$. Then, each of the $N$ parties is given a distinct share $s_i$ of $s$ as its partial decryption key.
To jointly decrypt $(a,b)$, parties aim to compute $as$ using their shares, which could be done by having each of them publish $as_i$. By linearity, we have $as = as_1 + … + as_N$. Yet, if a party publishes $as_i$, this provides a linear equation in it partial secret key $s_i$, which allows an attacker to recover $s_i$ by Gaussian elimination.
Instead, each party publishes $p_i = as_i + e_i$ where $e_i$ is some error sampled by the party decrypting. This corresponds to PartDec($s_i,(a,b)$). The small error term $e_i$ is referred to as the flooding error and allows to break the linear dependency between the output $p_i$ of PartDec($s_i,(a,b)$) and the party’s secret share $s_i$.
Still, adding up $p_1 + p_2 + … + p_N$ results in $a(s_1 + … + s_N) + e_1 + … + e_N$ $=$ $as + e’$ $\approx$ $as$ for some error $e’$, hence allowing to recover $\Delta m+e+e’$ by adding it to $b$. This corresponds to running FinDec($p_1,…,p_N,(a,b)$). Assuming $\Delta$ is large enough compared to $e+e’$, this still contains relevant information about $m$.
A central question for constructing ThFHE is then, how large should $e_i$ be for the scheme to be secure? On the one hand, the larger the $e_i$’s, the safier the scheme, since $p_i$ reveals less information about $s_i$. On the other hand, the larger the $e_i$’s, the noisier the result of the decryption $m+e+e’$.
On the size of the flooding error
As aforementioned, it is tempting to set $e_i = 0$ so that $e’ = 0$, but then $p_i$ reveals a linear equation in $s_i$ and the latter can be recovered by Gaussian elimination once a party has decrypted many messages. On the other hand, it has been known for long that choosing $e_i$ exponentially larger than the computation error $e$ guarantees security. Yet, setting $e_i$ so large requires to adjust the parameters of the FHE scheme in order to ensure that $\Delta m+e+e’$ still contains information about $m$: this leads to choosing a large modulus $q$. In conclusion, while $e_i$ is needed for security, its magnitude directly impacts the size of the ciphertext and therefore communication cost as well as computation cost. Over the last years, important efforts have been made to find solutions that reduce the magnitude of $e_i$ and to only rely on a moderate flooding error, polynomially larger than the computation error, have been made.
Limits for achieving ThFHE with moderate flooding error
Our first observation is that an exponentially large flooding is required in some basic settings. For instance, we provide an attack against the threshold variant of the B/FV FHE scheme, when the flooding error is not exponential. The attack exploits the fact that the computation error $e$ mostly depends on the underlying plaintexts when multiplications are involved. Hence, two computations that lead to the same result could still have vastly different computation errors if the inputs of the computation have different order of magnitude (e.g., 0*0 + 0*0 vs 100*1 - 2*50). To achieve security by simply adding a Gaussian flooding error during PartDec then requires the flooding error to be exponentially large.
A potential way to circumvent this issue would be to randomize the computation error during or after the computation, so that the computation noise is not so much dependent on the inputs of the computation. In this vein, Boudgoust and Scholl [BS23] attempted to construct ThFHE from FHE by combining moderate flooding error with circuit-private evaluation. A circuit-private FHE is an FHE scheme with the additional property that evaluating a function homomorphically should not reveal information about the function that has been computed (except the output of the computation) even to the decryptor, who knows the FHE secret key. In particular, this means that the computation error contains no information about the function being evaluated.
Unfortunately, we show that their construction is insecure by exhibiting a circuit-private FHE scheme that leads to an insecure ThFHE. Our attack relies on the fact that, while circuit-private evaluation removes information about the function being evaluated, the computation error could still contain sensitive information. In particular, we show that it can contain information about the secret key. This is not a problem for circuit-privacy, since the decryptor already knows the secret key and one only aims to protect the function that is evaluated, but it is a problem in ThFHE. If the computation error contains information about the secret key, the adversary can use the latter information to break privacy of honest parties.
The first take-away is that, as of today, all secure ThFHE schemes require adding an exponentially large flooding error during PartDec, and therefore require a large modulus and have large communication cost.
A low-communication solution in the trusted server model
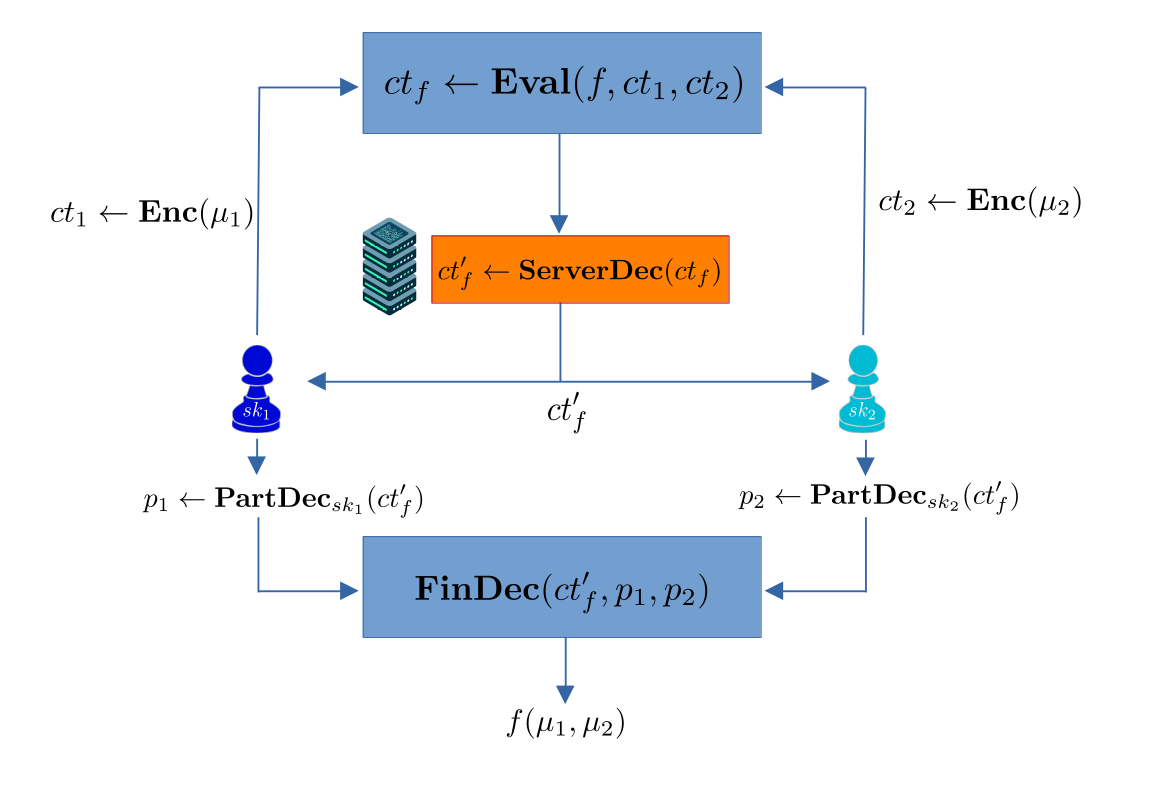
In order to circumvent the apparent need for exponential flooding error, we relax ThFHE by introducing an additional ServerDec algorithm. This algorithm is a public-key randomized algorithm, which is run by a trusted party (e.g., the server that runs the homomorphic computation) after the computation and before the decryptors run PartDec. It takes as input a ciphertext $(a,b)$ defined over some modulus $q$ and returns a new ciphertext $(a’,b’)$ defined over some modulus $q’$ and such that both ciphertexts decrypt to the same plaintext. The goal of ServerDec is to introduce additional randomness into a ciphertext before it gets decrypted, and we assume that the server cannot be corrupted so that this additional randomness remains unknown to the adversary.
Hence, a server-aided ThFHE scheme is a tuple (KeyGen, Enc, Eval, ServerDec, PartDec, FinDec), where ServerDec should be performed by a trusted party before PartDec is run by decryptors.
Looking back at our first example, the ciphertext $ct_f$ evaluated homomorphically is then processed by a trusted server using the ServerDec algorithm to obtain a new ciphertext $ct_f’$, which is distributively decrypted by parties. This is illustrated in the figure below.
While server-aided ThFHE is inherently weaker than ThFHE, it is still meaningful in some scenarios, for instance in scenarios (1) and (2) listed above. However, some applications of ThFHE are no longer possible with this notion (e.g., scenario (3) above, or more generally universal thresholdizers, see [BGG+18]).
Thanks to this additional randomness, we are able to construct server-aided ThFHE with tiny flooding errors during partial decryption. Our construction remains very similar to the basic one we already discussed, except that it relies on two distinct moduli: a large modulus $Q$ which allows exponential flooding errors, and a small modulus $q$.
Specifically, our construction encrypts data and performs homomorphic computation over the large modulus $Q$. The output of a computation is therefore a ciphertext $(a,b)$ over $Z_Q$ which satisfies $as+b = \Delta m + e \mod{Q}$ for some computation error $e$. The trusted server can then flood the computation error by adding an exponentially large error term $E$ to the ciphertext, i.e. by returning $(a,b+E)$ for $E \gg e$.
Then, the server can compress this ciphertext by Rescaling it to the small modulus $q$. This is done by having the server apply to the ciphertext the mapping $x \mapsto G_{round}(q/Q*x)$ where $G_{round}$ is a Gaussian rounding. This results in a ciphertext $(a’,b’)$ defined over $Z_q$ which satisfies $a’s + b’ = \Delta m + e’ \bmod q$ for some error $e’$.
Finally, we are able to show that it is possible to ensure security of this scheme by having parties adding a tiny flooding error $e_i$ in PartDec.
Security follows almost directly from the recent security analysis of lattice-based threshold public-key encryption by Micciancio and Suhl [MS25]. Specifically, the error $e’$ underlying $(a’,b’)$ is dominated by the rescaling of the exponentially large flooding error $E$ as well as the Gaussian rounding error, and therefore follows a publicly sampleable distribution. Hence, $(a’,b’)$ can essentially be seen as a fresh public-key encryption of $m$ and the security analysis for public-key encryption extends to our construction.
As a result, we obtain a server-aided ThFHE in which a tiny noise flooding error $e_i$ suffices to guarantee security, and as a consequence, a protocol for threshold delegation of computation on private data from multiple clients on a semi-honest server with low communication. The communication from the server to the decryptors is small thanks to our ServerDec algorithm which compresses the ciphertext. Also, the communication between decryptors is small as well since ciphertexts to be decrypted are small. The only communication that could be large is the one from the clients to the server, when they encrypt and upload ciphertexts for the computation. Furthermore, if there is a gap between the encrypted data and the encryption error (e.g., if we are dealing with discrete data), one can simply encrypt and compute over the smaller modulus $q$ and let the server bootstrap to the large modulus $Q$ at the end of the evaluation while still creating a large enough gap between the encrypted data and the computation error to tolerate noise flooding (this is somewhat similar to the “Switch-n-Squash” technique from [DDE+23]). Then, the server can run ServerDec to go back to the smaller modulus $q$. Doing so, all communications are now over the small modulus $q$, since ServerDec allows to go back to the small modulus $q$ before sending back the ciphertext to the clients for decryption. Hence, we have low communication (server-aided) threshold fully homomorphic encryption.
References
[BGG+18] Threshold Cryptosystems from Threshold Fully Homomorphic Encryption, D. Boneh, R. Gennaro, S. Goldfeder, A. Jain, S. Kim, P. M. R. Rasmussen, A. Sahai, CRYPTO 2018
[BS23] Simple Threshold FHE From LWE With Polynomial Modulus, K. Boudgoust and P. Scholl, ASIACRYPT 2024
[DDE+23] Noah’s Ark: Efficient Threshold-FHE Using Noise Flooding, M. Dahl, D. Demmler, S. El Kazdadi, A. Meyre, J.-B. Orfila, D. Rotaru, N. P. Smart, S. Tap, M. Walter, WAHC 2023
[LMSS22] Securing approximate homomorphic encryption using differential privacy, B. Li, D. Micciancio, M. Schultz, J. Sorrell, CRYPTO 2022
[MS25] Simulation-Secure Threshold PKE from LWE with Polynomial Modulus, D. Micciancio, A. Suhl, CiC 2025