Leveraging Discrete CKKS to Bootstrap in High Precision

• Written by Hyeongmin Choe (CryptoLab)
• Based on https://ia.cr/2025/1786 (CCS 2025)

TL;DR: We introduce a new high-precision CKKS bootstrapping method. It leverages a novel Integer Cleaning strategy inspired by the Discrete CKKS technique and is implemented using the Grafting technique. We highlight its main building blocks and discuss its efficiency.

---

Why High-Precision Bootstrapping Matters

CKKS bootstrapping aims to refresh ciphertexts by increasing their modulus while preserving the encrypted message, enabling further homomorphic computations. However, bootstrapping introduces an approximation error. Most existing implementations achieve 5–25 bits of precision, where the bit-precision can be defined as the negative base-2 logarithm of the worst-case error, measured across many runs.

Some advanced applications, however, require much smaller error to support stronger security properties such as Circuit Privacy and IND-CPA-D Security. It is also important for Threshold-FHE (see this blogpost). These are often achieved via noise flooding—adding large noise relative to the error before decryption—which blinds the secret-dependent error terms but also the lower bits of the message. To retain precision after flooding, the pre-flooding precision must be higher, typically 64–80 bits or more.

Supporting such high precision securely and efficiently is a key challenge in CKKS bootstrapping. In LLK+22¹, a high-accuracy polynomial approximation for modular reduction \(x \mapsto (x \bmod q)\) was introduced. This approximation enables high-precision CKKS bootstrapping, though it incurs enormous modulus consumption. Note that larger modulus consumption during bootstrapping leaves fewer levels available for subsequent computations, which necessitates more frequent bootstrappings and thus significantly increases the overall cost. BCC+22² introduced Meta-BTS, which achieves high precision by performing multiple sequential low-precision bootstrapping, at the cost of increasing latency linearly in the target precision. This approach also consumes slightly more modulus.

EvalRound+ Paradigm for High Precision

We follow the EvalRound+ paradigm as the first building block of high-precision CKKS bootstrapping. It differs slightly from the traditional CKKS bootstrapping. Let’s first recall the traditional CKKS bootstrapping pipeline:

\[\text{ModRaise} \rightarrow \text{CoeffsToSlots} \rightarrow \text{EvalMod} \rightarrow \text{SlotsToCoeffs}.\]

Assume a ciphertext encrypting a message \(m\) (or the coefficient vector of a polynomial) under modulus \(q_0\). In the ModRaise step, the ciphertext modulus is extended from \(q_0\) to a larger modulus \(Q\), which introduces an extra integer polynomial \(I\) multiplied by \(q0\). As a result, the ciphertext encrypts \(m + q_0I\), so an EvalMod step is needed to reduce the message modulo \(q_0\) and recover \(m\). To enable this modular reduction on the encrypted message, the ciphertext is first transformed from the coefficient domain to the slot domain via CoeffsToSlots. After EvalMod the result is mapped back to the coefficient domain using SlotsToCoeffs. Alternatively, one can place SlotsToCoeffs at the beginning. Here, we focus on the ModRaise-first variant, as the technical details are equivalent.

The EvalRound+ paradigm³, replaces EvalMod with a subroutine called EvalRound and branches into two parallel tracks. EvalRound⁴ is \(\text{EvalRound} = \text{Id} - \text{EvalMod}.\) That is, while EvalMod extracts the message \(m\) from \(m + q_0 I\), EvalRound extracts \(q_0 I\).

The EvalRound+ procedure begins with ModRaise and then splits into two tracks:

• the first track applies the standard CoeffsToSlots algorithm, and
• the second track uses a low-precision CoeffsToSlots* followed by EvalRound.

Then it subtracts the two resulting ciphertexts, and concludes with SlotsToCoeffs.

The two branches produce ciphertexts encrypting \(m + q_0 I\) and \(q_0 I\), respectively; subtracting them yields a ciphertext encrypting \(m\), which is then passed through SlotsToCoeffs to return to coefficient representation. Although the dual-track structure increases latency, it reduces modulus consumption, since only the second track dictates the modulus consumption and CoeffsToSlots* consumes much less modulus than the usual CoeffsToSlots algorithm.

To enable high-precision bootstrapping, one can upgrade CoeffsToSlots, EvalRound, and SlotsToCoeffs to their high-precision versions. Each requires larger scale factors (which is used for encodings to scale the real/complex messages) increasing modulus consumption. By contrast, CoeffsToSlots* can remain low-precision and consume significantly less modulus compared to the other bootstrapping components. This marks a key distinction from traditional CKKS bootstrapping, where high-precision CoeffsToSlots contributes to overall modulus consumption.

The main challenge is that high-precision bootstrapping still requires substantial modulus. In particular, EvalMod and EvalRound rely on polynomial approximations of \((x \bmod q)\) and \((x - (x \bmod q))\), respectively. Achieving higher accuracy requires higher-degree polynomials, whose multiplicative depth grows as \(\Theta(\log t)\), where \(t\) is the target bit-precision. Since scale factors grow as \(\Theta(t)\), overall modulus consumption typically scales as \(\Theta(t \log t)\).

Integer Cleaning from Discrete CKKS

Let’s take a closer look at the EvalRound procedure. When treating \(q_0\) as a new scale factor, EvalRound maps \((I+m/q_0)\) to \(I\). More precisely, an erroneous integer \(I + \varepsilon\) is mapped to a (much less) erroneous integer \(I + \varepsilon'\) where \(\varepsilon := m/q_0\) and \(\varepsilon' \ll \varepsilon\). As it cleans a noisy integer, we may call this functionality Integer Cleaning.

To reduce modulus consumption in high-precision bootstrapping, we introduce a novel Integer Cleaning algorithm based on this idea. The process involves:

1. Digit Extraction: Decompose the noisy integer \(I+\varepsilon\) into base-\(\beta\) digits: For \(I = \sum_{i=0}^{\ell} I_i \beta^i,\) each noisy digit \(I_i + \varepsilon_i\) is extracted and stored separately. This can be done by either:
   • using direct polynomial approximation, mapping \(I\) into \(I_i \in [0, \beta)\), or
   • mapping \(I\) into \(\exp(2i\pi I / \beta^\ell)\), the complex \(\beta^\ell\)-th roots of unity (as in CKKL24⁵), and decomposing the digits via interpolation (as in BKSS24⁶).
2. Iterative Digit Cleaning: Apply low-degree polynomials iteratively to each noisy digit \(I_i\), to refine its precision:
   • (\(\beta = 2\)) \(h_1(x) = 3x^2 - 2x^3\) from CKK20⁷, or
   • (\(\beta = 3\)) \(\frac{1}{3}(\bar{x}^2 + 4x - 2x^2\bar{x})\) from BKSS24⁶.

   These polynomials quadratically clean the bits or trits (ternary digits), refining a \(t\)-bit precision to around \(2t\)-bit. In the end, it returns the cleaned digits \(I_i + \varepsilon'_i\) with \(\varepsilon'_i \ll \varepsilon_i\). Note that for each iteration, the scale factor must be large enough to support the cleaned digit, which roughly squares after each iteration. This implies that early iterations (and Digit Extraction) can use much smaller scale factors (e.g., 25–35 bits) than the desired integer cleaning precision.

3. Recombination: Combine the cleaned digits \(I_i + \varepsilon'_i\) to reconstruct the cleaned integer \(I + \varepsilon'\). This requires only integer multiplications and additions, with no extra modulus consumption.

Suppose the input \(I + \varepsilon\) to the Integer Cleaning algorithm has \(t\)-bit precision (i.e., \(|\varepsilon| \leq 2^{-t}\)). Then, with \(\text{iter}\) iterations of Digit Cleaning, the algorithm outputs an integer with \(\Theta(2^{\text{iter}} \cdot t)\) bits of precision.

Grafting

We leverage Grafting⁸ to efficiently support heterogeneous (i.e., small) scale factors without incurring additional RNS moduli or performance loss. This allows our implementation to achieve modulus-efficient and high-performance bootstrapping. For further details on RNS-CKKS and Grafting, see this blogpost.

Putting It All Together

The new CKKS bootstrapping is built on the EvalRound+ paradigm with the Integer Cleaning strategy and employs the Grafting technique. We note that the Integer Cleaning parts can be further optimized using a so-called Thrifty approach detailed in the paper.

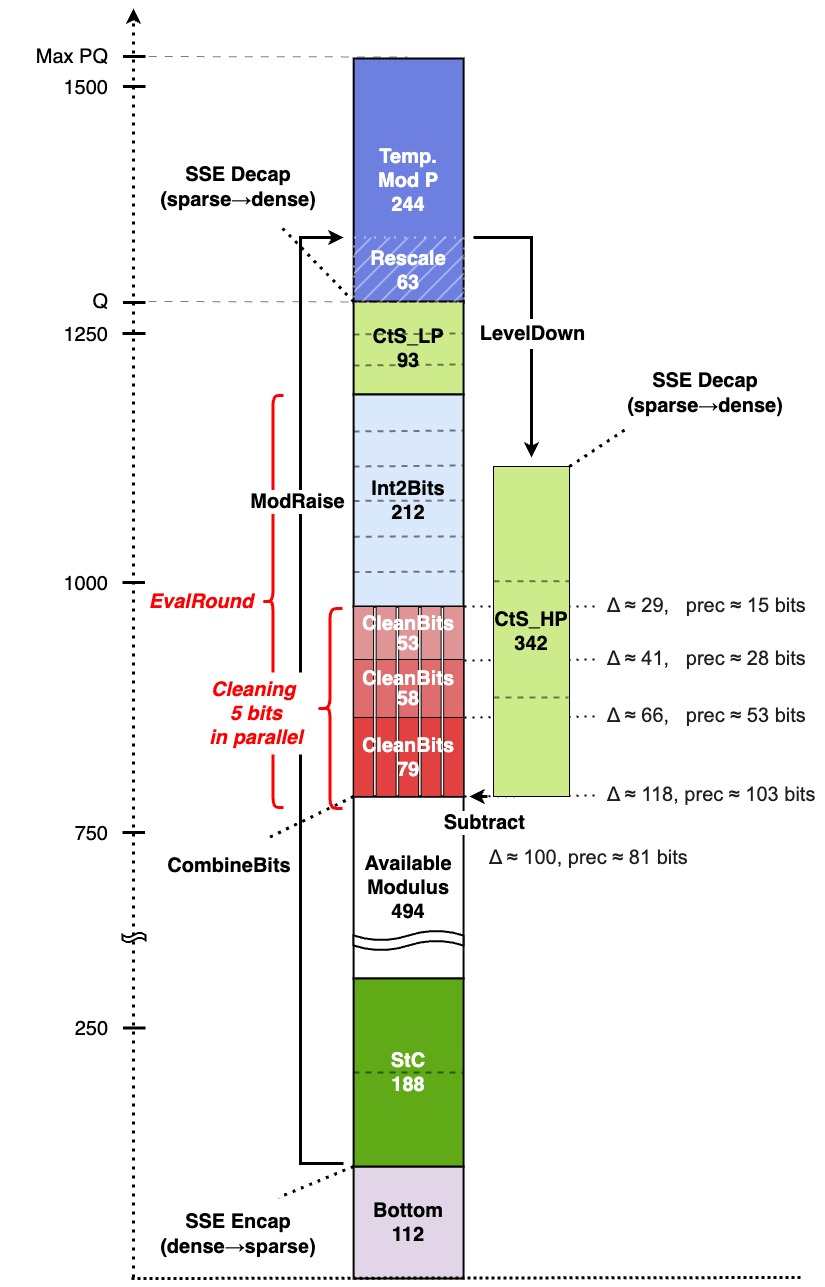
In our proof-of-concept implementation, we used a ring dimension of \(N=2^{16}\) with full-slot messages. With bit decomposition (\(\beta = 2\)), the direct approximation method for bit extraction, and three iterations of bit-cleaning, our bootstrapping achieved 81 bits of precision. We compared this with Meta-BTS, which requires four sequential bootstraps to reach similar accuracy. Our bootstrapping achieved a 1.64× speedup, while still leaving 494 bits available for homomorphic computations.

We note that the bootstrapping scales naturally with the desired precision, thanks to its iterative nature. By adjusting the number of digit-cleaning iterations, one can flexibly target either lower or higher bootstrapping precisions. For instance, adding one more iteration yields roughly 150 bits of precision still at \(N=2^{16}\), with only a modest increase in latency.

In summary, the new bootstrapping method, combining EvalRound+, Integer Cleaning, and Grafting, enables high-precision CKKS bootstrapping that is modulus-efficient and high-performance, offering a practical solution for advanced homomorphic encryption applications.

References