Ciphertext-Ciphertext Matrix Multiplication: Fast for Large Matrices

• Written By Jai Hyun Park
• Based on https://ia.cr/2025/448 (Eurocrypt 2025)

TL;DR: We propose fast ciphertext-ciphertext matrix multiplication (CC-MM) algorithms for large matrices. Our algorithms consist of plaintext matrix multiplications (PP-MM) and ciphertext matrix transpose algorithms (C-MT). We introduce and utilize new fast C-MT algorithms for large matrices. By leveraging high-performance BLAS libraries to accelerate PP-MM, we implement large-scale CC-MM with substantial performance improvements.

---

The Matrix Has You

“The Matrix is everywhere. It is all around us. Even now, in this very room.” — Morpheus, The Matrix (1999), written by Lilly & Lana Wachowski

Matrix multiplication (PP-MM) is one of the central tasks in machine learning (ML). In particular, for large ML models, accelerating large matrix multiplication is important as its cost grows cubically with the dimension of the matrix. There exist many highly optimized open linear algebra libraries (BLAS libraries). On my machine using a single thread CPU, the OpenBLAS library took 1.47 seconds to multiply two large \(4096\times 4096\) matrices, which was 30x faster than my schoolbook implementation.

Matrix multiplication on encrypted data plays an important role in privacy-preserving ML, when a server trains or performs inference on ML models using encrypted data. For example, when using homomorphic encryption for large language models, one needs to multiply matrices of various dimensions either in encrypted or unencrypted form. For the multiplication between plaintext and ciphertext matrices (PC-MM), a recent work BCHPS24¹ significantly improved the efficiency compared to the state of the art, taking 17.1 seconds for \(4096\times 4096\) matrices on an Intel Xeon Gold 6242 CPU running at 2.80GHz, using a single thread.

However, ciphertext-ciphertext matrix multiplication (CC-MM) has been much slower than PC-MM and PP-MM. A notable work JKLS19² took 0.6 seconds for multiplying two \(64\times 64\) matrices on an Intel Core i9 CPU with 4 cores rated at 2.3GHz. If one naively utilizes JKLS19 for \(4096\times 4096\) matrices, it takes more than 19 hours. This is not desirable. Note that most of the current CC-MM implementations are based on JKLS19 or its variants.

As Fast As Matrix Multiplications in Clear

Reduction to PP-MM

A lower bound for the cost of PC-MM and CC-MM is the cost of PP-MM: if CC-MM becomes faster than PP-MM, we should replace all existing PP-MM codes with this new CC-MM implementation. How close can PC-MM and CC-MM be to PP-MM?

BCHPS24 suggested a strategy to answer this question by providing a reduction from PC-MM to PP-MMs. Precisely, they perform PC-MM by using multiple PP-MMs with other minor computations. It makes PC-MM comparable to PP-MM up to small constant factors. Note that the impact of this reduction strategy is significant in practice; JKLS19 would take several hours for large matrices even though the JKLS19 algorithm provides a good asymptotic complexity. The reduction allows to exploit BLAS-based PC-MM.

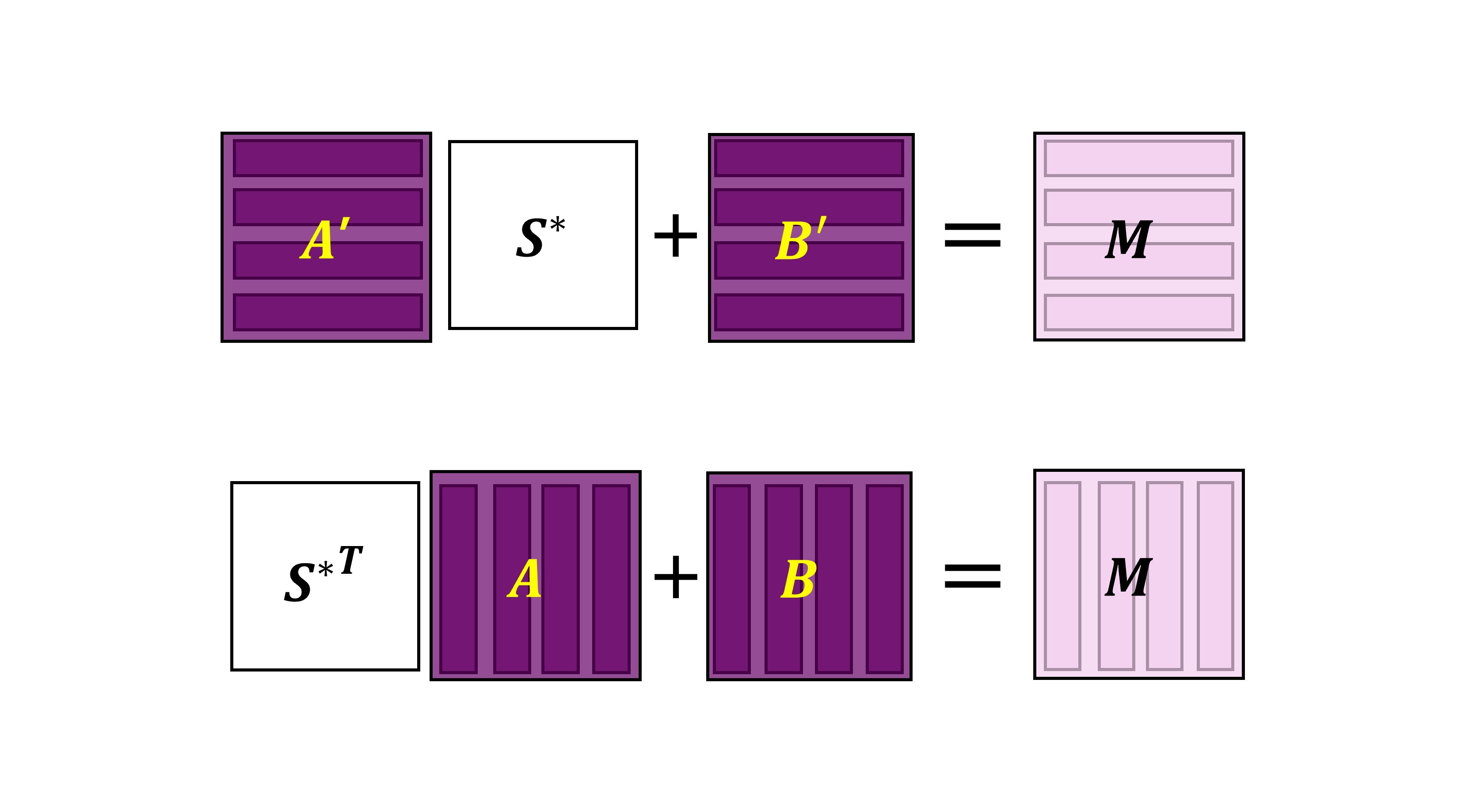
The reduction introduced in BCHPS24 starts with a simple equation borrowed from LZ22³. A bundle of coefficient-encoded CKKS ciphertexts encrypting each row of a plaintext matrix \(\textbf{V}\) corresponds to a pair of plaintext matrices \((\textbf{A}, \textbf{B})\) satisfying

\[\textbf{A} \cdot \textbf{S}^*+\textbf{B}~\approx~\textbf{V},\]

where \(\textbf{S}^*\) is a structured matrix determined by the ciphertext format⁴ and the secret. Once multiplying a plaintext matrix \(\textbf{U}\) to above equation, it becomes

\[(\textbf{U}\cdot\textbf{A})\cdot \textbf{S}^* +(\textbf{U}\cdot\textbf{B})~\approx~\textbf{U}\cdot\textbf{V}.\]

This process results in CKKS ciphertexts that encrypt each row of the product matrix \(\textbf{U}\cdot\textbf{V}\). This is a reduction from PC-MM to two plaintext matrix multiplications \(\textbf{U}\cdot\textbf{A}\) and \(\textbf{U}\cdot\textbf{B}\). A part of the results from BCHPS24 is the utilization of BLAS PP-MM libraries for various dimensional PC-MM tasks.

What about CC-MM?

One may ask whether we can reduce CC-MM to PP-MMs in the same way. However, CC-MM is not as easy as PC-MM. Suppose we have two bundles of CKKS ciphertexts that decrypt to \(\textbf{U}\) and \(\textbf{V}\), respectively. We can represent them as two pairs of matrices \((\textbf{A}_{\textbf{U}}, \textbf{B}_\textbf{U})\) and \((\textbf{A}_\textbf{V}, \textbf{B}_\textbf{V})\) such that \(\textbf{A}_\textbf{U} \cdot \textbf{S}^*+\textbf{B}_\textbf{U}~\approx~\textbf{U}\) and \(\textbf{A}_\textbf{V} \cdot \textbf{S}^*+\textbf{B}_\textbf{V}~\approx~\textbf{V}\). Once we multiply them, we obtain

\[\textbf{U}\cdot\textbf{V}~\approx~(\textbf{A}_\textbf{U} \cdot \textbf{S}^*\cdot \textbf{A}_\textbf{V} \cdot \textbf{S}^*)+(\textbf{A}_\textbf{U} \cdot \textbf{S}^*\cdot\textbf{B}_\textbf{V})+(\textbf{B}_\textbf{U}\cdot \textbf{A}_\textbf{V} \cdot \textbf{S}^*)+(\textbf{B}_\textbf{U}\cdot \textbf{B}_\textbf{V}).\]

In contrast to PC-MM, it does not reduce to PP-MMs between \(\textbf{A}_\textbf{U}, \textbf{B}_\textbf{U}, \textbf{A}_\textbf{V}\), and \(\textbf{B}_\textbf{V}\). The secret matrices \(\textbf{S}^*\) appears in the middle of the multiplications. To interpret this using CKKS ciphertexts, one may want to swap the order of matrix multiplication (e.g., \(\textbf{A}_\textbf{U} \cdot\textbf{B}_\textbf{V}\cdot \textbf{S}^*\) instead of \(\textbf{A}_\textbf{U} \cdot \textbf{S}^*\cdot\textbf{B}_\textbf{V}\) ). However, matrix multiplication is not commutative.

Ciphertext Matrix Transpose

Here is an approach to solve the above problem. For each \(\textbf{S}^*\cdot\textbf{M}\), suppose we can find an appropriate \(\textbf{M}'\) such that \(\textbf{S}^*\cdot\textbf{M}~=~\textbf{M}'\cdot\textbf{S}^*\). Once we find it, we replace \(\textbf{S}^*\cdot\textbf{M}\) with \(\textbf{M}'\cdot\textbf{S}^*\). Then, the above equation turns into

\[\textbf{U}\cdot\textbf{V}~\approx~(\textbf{A}_\textbf{U} \cdot \textbf{A}_\textbf{V}' )\cdot {\textbf{S}^*}^2+(\textbf{A}_\textbf{U} \cdot\textbf{B}_\textbf{V}'+\textbf{B}_\textbf{U}\cdot \textbf{A}_\textbf{V})\cdot \textbf{S}^*+(\textbf{B}_\textbf{U}\cdot \textbf{B}_\textbf{V}).\]

This reduces CC-MM to four PP-MMs, \(\textbf{A}_\textbf{U} \cdot \textbf{A}_\textbf{V}'\) , \(\textbf{A}_\textbf{U} \cdot\textbf{B}_\textbf{V}'\), \(\textbf{B}_\textbf{U}\cdot \textbf{A}_\textbf{V}\), and \(\textbf{B}_\textbf{U}\cdot \textbf{B}_\textbf{V}\), and a relinearization.

Let us take a step back to understand what \({\textbf{S}^*}\cdot\textbf{M}\) means. A bundle of CKKS ciphertexts encrypting each column of a plaintext matrix \(\textbf{V}\) corresponds to a pair of matrices \((\textbf{A}, \textbf{B})\) such that

\[{\textbf{S}^*}^T\cdot \textbf{A} +\textbf{B}~\approx~\textbf{V}.\]

Thereby, finding \((\textbf{A}', \textbf{B}')\) from \((\textbf{A},\textbf{B})\) such that \(\textbf{A}'\cdot\textbf{S}^*+\textbf{B}'~\approx~{\textbf{S}^*}^T\cdot \textbf{A} +\textbf{B}~\approx~\textbf{V}\) is equivalent to the ciphertext matrix transpose (C-MT) problem. Even though this is not exactly the same as finding \(\textbf{M}'\) from \(\textbf{M}\) that \(\textbf{S}^*\cdot\textbf{M}~=~\textbf{M}'\cdot\textbf{S}^*\), the above argument hints that a fast C-MT algorithm would be useful for fast CC-MM.

Algebraically, the C-MT is related to converting \(\{m_i(X)~\approx~ \sum_j \textbf{M}_{i,j}X^j \}_i\) into \(\{m_j'(X) ~\approx~ \sum_i \textbf{M}_{i,j}X^i \}_j\). We can use algebraic and algorithmic ideas to devise efficient C-MT algorithms. Please refer to Section 3 of Park25⁵ for the details. The paper introduces two C-MT algorithms, one focusing on the latency (Section 3) and the other focusing on the key size (Section 5). Independently, Craig Gentry has also sketched another C-MT approach involving bivariate polynomials in a recent talk in FHE.org conference.⁶

Ciphertext-Ciphertext Matrix Multiplication

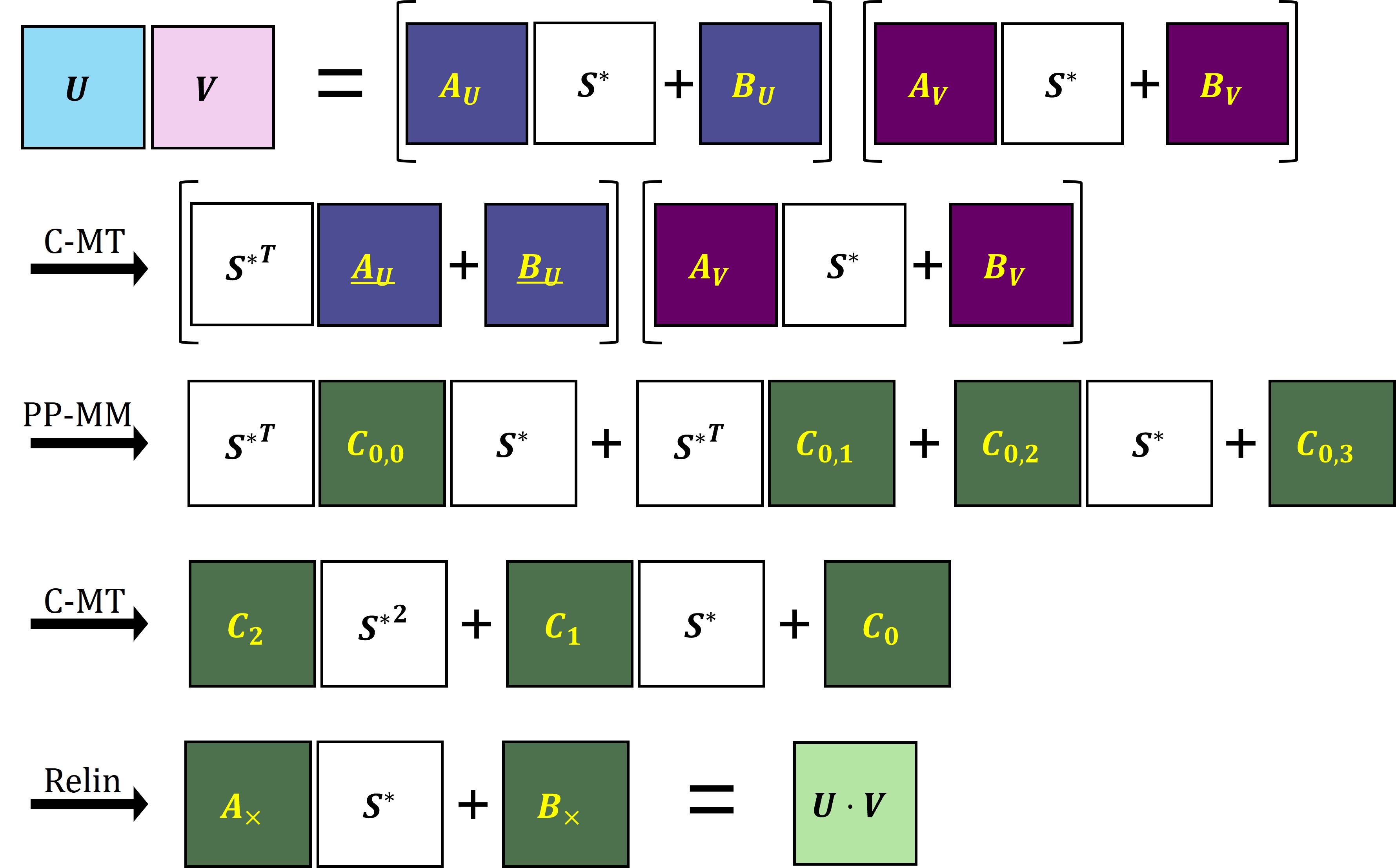
Finally, we put it all together to devise a fast CC-MM algorithm for large matrices. Assume that we are given two pairs of matrices \((\textbf{A}_\textbf{U}, \textbf{B}_\textbf{U})\) and \((\textbf{A}_\textbf{V}, \textbf{B}_\textbf{V})\) such that \(\textbf{A}_\textbf{U} \cdot \textbf{S}^*+\textbf{B}_\textbf{U}~\approx~\textbf{U}\) and \(\textbf{A}_\textbf{V} \cdot \textbf{S}^*+\textbf{B}_\textbf{V}~\approx~\textbf{V}\). As previously mentioned, it implies that

\[\textbf{U}\cdot\textbf{V}~\approx~(\textbf{A}_\textbf{U} \cdot \textbf{S}^*+\textbf{B}_\textbf{U})\cdot(\textbf{A}_\textbf{V} \cdot \textbf{S}^*+\textbf{B}_\textbf{V}).\]

The CC-MM algorithm follows the following steps.

1. It first performs C-MT on \((\textbf{A}_\textbf{U}, \textbf{B}_\textbf{U})\), obtaining a pair of matrices \((\underline{\textbf{A}}_\textbf{U}, \underline{\textbf{B}}_\textbf{U})\) that satisfies \({\textbf{S}^*}^T\cdot\underline{\textbf{A}}_\textbf{U}+\underline{\textbf{B}}_\textbf{U}\approx\textbf{U}\). Then,

   \[\textbf{U}\cdot\textbf{V}~\approx~({\textbf{S}^*}^T\cdot\underline{\textbf{A}}_\textbf{U}+\underline{\textbf{B}}_\textbf{U})\cdot(\textbf{A}_\textbf{V} \cdot \textbf{S}^*+\textbf{B}_\textbf{V}).\]

2. It computes four PP-MMs, \(\underline{\textbf{A}}_\textbf{U} \cdot \textbf{A}_\textbf{V}\), \(\underline{\textbf{A}}_\textbf{U} \cdot \textbf{B}_\textbf{V}\), \(\underline{\textbf{B}}_\textbf{U}\cdot \textbf{A}_\textbf{V}\), and \(\underline{\textbf{B}}_\textbf{U}\cdot \textbf{B}_\textbf{V}\), using fast BLAS libraries. Let \(\textbf{C}_{0,0}\) , \(\textbf{C}_{0,1}\), \(\textbf{C}_{1,0}\), \(\textbf{C}_{1,1}\) be the output matrices, respectively. Then, it holds that

   \[\textbf{U}\cdot\textbf{V}~\approx~{\textbf{S}^*}^T\cdot \textbf{C}_{0,0} \cdot \textbf{S}^*+{\textbf{S}^*}^T\cdot\textbf{C}_{0,1}+\textbf{C}_{1,0}\cdot \textbf{S}^*+\textbf{C}_{1,1}.\]

3. It transposes \((\textbf{C}_{0,0}, \textbf{0})\) and \((\textbf{C}_{0,1}, \textbf{0})\) to find matrices that \({\textbf{S}^*}^T\cdot \textbf{C}_{0,0}\approx \textbf{A}\cdot\textbf{S}^*+\textbf{B}\) and \({\textbf{S}^*}^T\cdot \textbf{C}_{0,1}\approx \textbf{A}'\cdot\textbf{S}^*+\textbf{B}'\). Since each entry of \(\textbf{S}^*\) is small, it impliest that \({\textbf{S}^*}^T\cdot \textbf{C}_{0,0}\cdot \textbf{S}^*\approx \textbf{A}\cdot{\textbf{S}^*}^2+\textbf{B}\cdot \textbf{S}^*\). After several matrix additions, it obtains three matrices \((\textbf{C}_2, \textbf{C}_1, \textbf{C}_0)\) such that

   \[\textbf{U}\cdot\textbf{V}~\approx~\textbf{C}_2 \cdot{\textbf{S}^*}^2+\textbf{C}_1\cdot\textbf{S}^*+\textbf{C}_0.\]

4. It relinearizes and rescales each row of \((\textbf{C}_2, \textbf{C}_1, \textbf{C}_0)\) as is done usually in CKKS. It finally obtains a pair of matrices \((\textbf{A}_\times, \textbf{B}_\times)\) such that

   \[\textbf{U}\cdot\textbf{V}~\approx~\textbf{A}_\times\cdot\textbf{S}^*+\textbf{B}_\times.\]

   This corresponds to CKKS encryptions of the product matrix \(\textbf{U}\cdot\textbf{V}\), completing the CC-MM.

Note that the algorithm consists of three C-MTs and four PP-MMs. The cost of C-MT is asymptotically minor compared to the cost of PP-MM, and one can fully utilize the high efficiency of BLAS libraries for the PP-MMs. The implementation in Park25⁵ took 85.2 seconds to multiply two \(4096\times 4096\) encrypted matrices on an Intel Xeon Gold 6242 CPU running at 2.80GHz, using a single thread. This is a huge improvement compared to the previous 19 hours. Park25⁵ introduces another CC-MM algorithm that focuses on the key size, so take a look if you are interested!

Next Steps

In the more recent work BCHPS25⁷, which is an extended and consolidated journal version of this paper and BCHPS24, my colleagues and I introduce fast CC-MM algorithms with pre-computations. As a future direction, it would be interesting to explore whether CC-MM for small-dimensional matrices can be reduced to PP-MM of the same dimensions, without any pre-computations.