A Novel Asymmetric BSGS Polynomial Evaluation Algorithm under Homomorphic Encryption

Written by Qingfeng Wang (Institute of Information Engineering, Chinese Academy of Sciences)
Based on https://doi.org/10.1145/3708821.3710822 (ASIACCS 2025)

TL;DR: We introduce a new polynomial evaluation algorithm under homomorphic encryption, namely the Asymmetric BSGS Algorithm. It is a generalization and specialization of the original Baby-Step Giant-Step algorithm in the leveled FHE computation model. Leveraging the observation that there is a difference in multiplicative depth between the baby-step set and the giant-step set, this algorithm significantly reduces the number of modulus and key switches required for dense polynomial evaluation from $O(\sqrt{d})$ to $O(d^{1/t})$, by adjusting the set decomposition method and relaxing the control of noise growth and ciphertext size in some calculations. Here, $d$ is the polynomial degree and $t$ is a small constant which, according to our experiments, is recommended to be chosen as $4$.

1. How to Compute Polynomial Evaluation?

Polynomial evaluation is one of the most crucial tasks in the field of computing. This is particularly true in leveled FHEs, as they only support homomorphic addition, homomorphic multiplication, and some automorphisms related to SIMD packing. Almost all functions are either interpolated (in BGV/BFV) or approximated (in CKKS) with the use of specific polynomials.

So, how can we efficiently compute polynomial evaluation? For polynomials that can be factored into sparse factors, such as $f(X) = (x^3+1)^{16}\cdot(x^{32}+x-1)$, we can compute the evaluation of each sparse-coefficient polynomial separately and then multiply them together. Thus, the computational cost is relatively low, although the multiplication depth may not be optimal. However, most polynomials are difficult or even impossible to factor into sparse factors. One can only use general polynomial evaluation algorithms to deal with them, among which the most well-known is the BSGS algorithm¹.

Briefly speaking, for a degree-$d$ polynomial $f(X) = \sum_{i}f_{i}X^{i}$, the BSGS algorithm selects two integers, $k\approx m\approx\sqrt{d}$, such that $km > d$. Then the coefficients of $f(X)$ can be partitioned into $m$ intervals of length at most $k$, namely

\[f(X)=\sum_{j = 0}^{m - 1}f^{(j)}(X)\cdot(X^{k})^{j},\]

where each $f^{(j)}(X)=\sum_{i = 0}^{k-1}f_{jk + i}X^{i}$ is a polynomial of degree less than $k$.

Given a value $x$, pre-compute $S_1 := \{1,x,\cdots,x^{k-1}\}$ (which we call the baby-step set) and $S_2 := \{1,z,\cdots,z^{m-1}\}$ (which we call the giant-step set), where $z := x^k$. Then the computation of all $y_j := f^{(j)}(x)$ is merely a linear combination of the elements in $S_1$, and this can be efficiently computed in leveled FHE. Finally, by multiplying the $y_j$ with the elements in $S_2$ and then summing them up, the computation of $f(x)$ can be completed.

The above-mentioned algorithm takes $3\sqrt{d}$ non-scalar multiplications: computing $S_1$, computing $S_2$, and the final multiplication and accumulation each take $\sqrt{d}$ non-scalar multiplications. If we use Horner’s rule, the computation of $S_2$ can be omitted, but at the cost of increasing the multiplication depth to the order of $\sqrt{d}$. The recursive variant of the BSGS algorithm, the Paterson-Stockmeyer algorithm, only requires $\sqrt{2d}+O(\log d)$ non-scalar multiplications and has a multiplicative depth of logarithmic order.

It has been proven that a general polynomial evaluation algorithm requires at least $\sqrt{d}$ non-scalar multiplications¹, so it seems that there is no way to further improve the performance.

2. We Can Do Better!

We need to emphasize that there are significant differences between the leveled FHE computation model and the classical computation model. In the classical computation model, multiplication is an atomic operation, and there is no concept of “levels” for data.

However, in the leveled FHE computation model, homomorphic multiplication consists of three distinct operations with different purposes.

Tensor product: A ciphertext $\mathbf{ct} \in \mathcal{R}_q[\mathbf{S}]$ is a polynomial over the cyclotomic ring $\mathcal{R}_q$ with respect to the variable $\mathbf{s} \in \mathcal{R}_q$, and its (noisy) plaintext is its evaluation $\mathbf{ct}(\mathbf{s}) = \textbf{m}+\textbf{e} \in \mathcal{R}_q$. Multiplying two ciphertexts then realizes the multiplication of the two underlying plaintexts. In a typical setting, the asymptotic complexity of the tensor product is linear in terms of the security parameter, and the cost of tensor product amounts to less than 5% of that of homomorphic multiplication in practice.
Modulus switching: When performing the tensor product, the ciphertext noise $\mathbf{e} \in \mathcal{R}_q$ is also multiplied, and its growth rate is proportional to the norm of $\mathbf{e}$. By dividing by a rescaling factor in the cyclotomic field $\mathcal{K}\supset\mathcal{R}$ and then rounding to $\mathcal{R}$ to discard the lower-order bits of the noise $\mathbf{e}$, the noise growth can be effectively controlled. And modulus switching endows ciphertexts with levels. The asymptotic complexity of modulus switching is quasi-linear with respect to the security parameter, and the cost of modulus switching typically constitutes approximately 20% in homomorphic multiplication.
Relinearization: Because polynomial multiplication over $\mathcal{R}_q[\mathbf{S}]$ will increase the degree of the ciphertext, we need use key switching to linearize the ciphertext polynomial. This is also of quasi-linear complexity with respect to the security parameter, and it is usually the most costly one, especially when the ciphertext size increases.

Now, let’s consider what is special about implementing the BSGS algorithm in leveled FHEs. Horner’s rule would imply depth proportional to the square root of the degree, so is excluded. Given the ciphertext of $x$, using a binary-tree approach to pre-compute the ciphertexts of $S_1$ and $S_2$ requires $\sqrt{d}$ standard homomorphic multiplications respectively. In the process of multiplying the $y_j$ with the elements in $S_2$ and accumulating, the lazy technique, which takes advantage of the commutativity and associativity between the above-mentioned three operations and addition, can be used to combine some modulus and key switches. Altogether, approximately $2\sqrt{d}$ modulus and key switches are required.

The figure below shows the homomorphic evaluation process of a 32-degree polynomial, where $k = m = 6$.

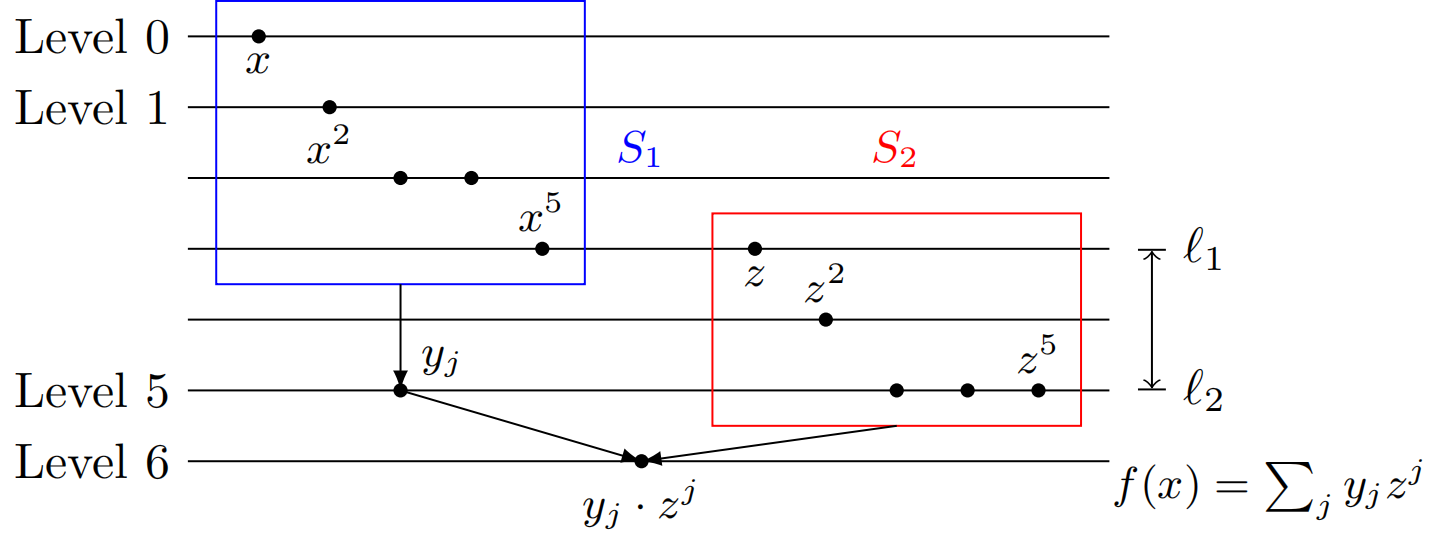
We observe that the ciphertexts of $S_1$ have a much shallower ciphertext level than those of $S_2$. Specifically, the multiplicative depth of the ciphertexts of $S_1$ is $\ell_1=\left\lceil \log (k - 1) \right\rceil$, and the multiplicative depth of the ciphertexts of $S_2$ is $\ell_2=\left\lceil \log (km - k) \right\rceil$. The difference between the two is $\ell_2-\ell_1\approx\frac{1}{2}\cdot\log d$, which is half of the overall multiplicative depth. We note that the noise control for the ciphertexts of set $S_1$ does not actually need to be so strict. As long as the multiplicative depth of $S_1$ is not greater than that of $S_2$, the multiplicative depth of the final calculation result will not change.

How can we make full use of this difference in multiplicative depth? During the construction of $S_1$, given $t = \ell_2-\ell_1+1$ ciphertexts located at most at the $\ell_1$-th layer, it is tempting to evaluate their tensor products without performing modulus switching. At this time, the depth of the calculated $S_1$ will not exceed $\ell_2$, and the computational efficiency is significantly improved.

Since the size of $S_2$ is $\sqrt{d}$, the overall number of modulus switches is still $O(\sqrt{d})$, but this is sufficient to provide us with an optimization direction. To achieve improvement in asymptotic complexity, we suggest to:

Adjust the relative sizes of $S_1$ and $S_2$.
Further decompose $S_1$ into some small sets.

3. Asymmetric BSGS Algorithm

3.1 Preliminary Version

First, we introduce “set multiplication”, which is used to simplify the description of set decomposition in the algorithm. Given two sets $S$ and $S'$, which are subsets of a multiplicative group $(G,\cdot)$. Define $S \odot S':=\{s \cdot s' \mid s\in S, s'\in S'\} \subseteq G$.

For a set $S := \{1,x,\cdots,x^d\}$, the BSGS algorithm considers two sets $S_1$ and $S_2$ of approximately the same size, such that $S\subseteq S_1\odot S_2$. We generalize it to: $S \subseteq S_1^{(0)} \odot \cdots \odot S_1^{(t - 1)} \odot S_2,$

such that $|S_1^{(j)}| = O(d^{1/t})$ and $|S_2|\leq2^{t - 1}=O(1)$, where $t$ is a small integer.

Most importantly, we ensure that the multiplicative depth of $S_2$ is $t - 1$ levels higher than that of $S_1^{(j)}$. Then,

First, use the binary-tree method to construct $S_1^{(j)}$ and $S_2$.
Second, reconstruct $S_1$ based on $S_1^{(j)}$ and calculate $y_j := f^{(j)}(x)$, without performing modulus switching during this process.
Finally, calculate $f(x)$ based on $y_j$ and $S_2$.

Since the multiplicative depth of $S_1$ calculated in step 2 does not exceed the multiplicative depth $\ell_2$ of $S_2$, the multiplicative depth spent by the above algorithm is $\ell_2 + 1$, which is the same as that of the original BSGS algorithm. Let’s briefly analyze the number of modulus switches spent by this algorithm: Step 1 requires $t\cdot O(d^{1/t})+2^{t-1}$ modulus switches, step 2 no longer requires modulus switches, and step 3 requires $O(1)$ modulus switches. In total, it spends $O(d^{1/t})$ modulus switches.

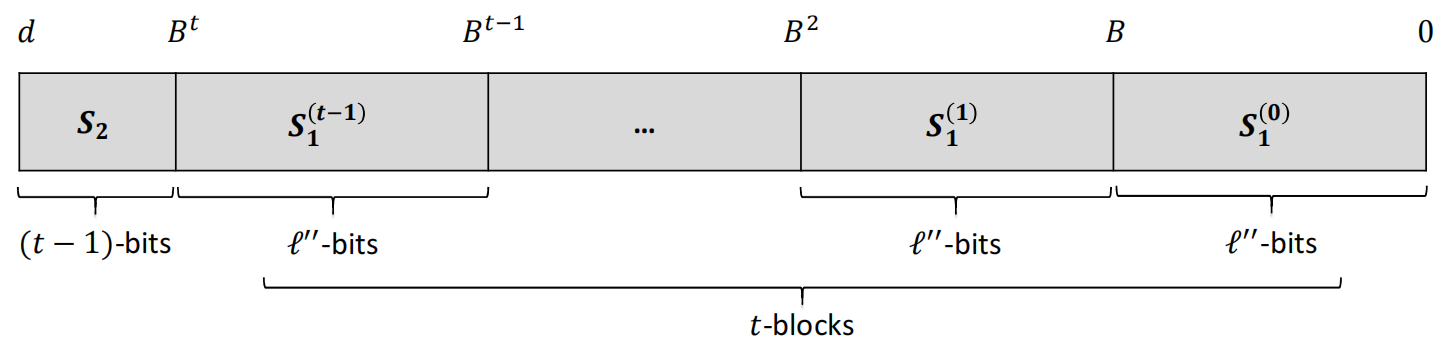
The decomposition of the set $S$ is not unique. By generalizing the decomposition method in the original BSGS, we present a simple method based on digit decomposition. Suppose $\ell=\lceil\log d\rceil$, set $\ell'=\ell-(t - 1)$, $\ell''=\ell'/t$ and $B = 2^{\ell''}$. Define the sets

\[S_1^{(j)}:=\{x^e\mid e = i\cdot B^j,\, i = 0,\cdots,B - 1\},\, j = 0,\cdots,t - 1\]

and

\[S_2:=\{x^e\mid e = i\cdot B^t,\, i = 0,\cdots,\lfloor d/B^t\rfloor\},\]

where the multiplicative depth of $S_1^{(j)}$ is $(j + 1)\cdot\ell''\leq\ell'$, which is $(t - 1)$ levels shallower than the multiplicative depth $\ell$ of the set $S_2$. The figure below shows the relative relationship of the multiplicative depths of each set.

3.2 Complete Version

In the above-mentioned algorithm, there are still two directions for optimization:

Reduce the number of key switches. Since $t$ is a small integer, even if no relinearization is performed in step 2, the ciphertexts in the obtained $S_1$ are polynomials in $\mathcal{R}_q[\mathbf{S}]$ with degree at most $t$. We postpone all relinearizations to step 3, utilizing the lazy technique along with a larger key-switching key.
Reduce the number of tensor products. The size of the set $S_1$ is $O(d^{1/t})^t = O(d)$, so step 2 requires the computation of $O(d)$ tensor products. This can be reduced to $O(\sqrt{d})$ by re-applying the BSGS algorithm, which we term the ”Internal BSGS Subroutine”.

Specifically, let $t'=\lceil t/2\rceil$ and define

\[\bar{S}_1 = \{x^e\mid e = 0,\cdots,B^{t'}-1\}\]

and

\[\hat{S}_1=\{x^e\mid e = i\cdot B^{t'},\, i = 0,\cdots,B^{t - t'}-1\}.\]

Then, it can be proven that $\bar{S}_1\subseteq S_1^{(0)}\odot\cdots\odot S_1^{(t'-1)}$, $\hat{S}_1\subseteq S_1^{(t')}\odot\cdots\odot S_1^{(t - 1)}$ and $S_1\subseteq \bar{S}_1\odot\hat{S}_1$, where $|\bar{S}_1| \approx |\hat{S}_1| = O(\sqrt{d})$. Similar to the original BSGS algorithm, based on the pre-computed $\bar{S}_1$ and $\hat{S}_1$, the $y_j$ in step 2 can be calculated rapidly.

Given a polynomial $f(X)=\sum_j f^{(j)}(X)\cdot(X^{B^t})^j$ and the ciphertext of the value $x$, the steps of the asymmetric BSGS algorithm are as follows:

First, compute $S_1^{(j)}$ and $S_2$, which costs $O(d^{1/t})$ standard homomorphic multiplications.
Second, construct $\bar{S}_1$ and $\hat{S}_1$ based on $S_1^{(j)}$, and then use the Internal BSGS Subroutine to compute $y_j := f^{(j)}(x)$. During this process, only $O(\sqrt{d})$ tensor products are performed.
Finally, perform modulus switching and relinearization on $y_j$, and then compute $f(x)$ based on $S_2$. Here, it costs $O(1)$ standard homomorphic multiplications.

This provides a description of the high-level abstraction of the asymmetric BSGS algorithm.

3.3 Specific Implementation

Due to the fact that different leveled FHEs adopt different encoding strategies, there are subtle differences in the specific implementation of the asymmetric BSGS algorithm.

BGV uses LSB encoding and NTT packing, with explicit ciphertext levels and modulus switching. The asymmetric BSGS algorithm fully adheres to the description in the previous subsection.
CKKS uses fixed-point number encoding and DFT packing, with explicit ciphertext levels, and modulus switching is replaced by rescaling. The asymmetric BSGS algorithm also fully follows the description in the previous subsection, and its computational accuracy is close to that of the original BSGS algorithm.
BFV uses MSB encoding and NTT packing, and modulus switching is implicitly performed during the tensor product, making it difficult to actively relax the noise control. For Step 2, we suggest to first convert all the BFV ciphertexts in $S_1^{(j)}$ to BGV ciphertexts², then compute the tensor products, and finally convert $\bar{S}_1$ and $\hat{S}_1$ back to BFV ciphertexts.

3.4 Complexity Analysis

The following table compares the asymptotic complexity of the asymmetric BSGS algorithm with that of the original BSGS algorithm and its recursive variant (Paterson-Stockmeyer algorithm).

A recent article³ proposed an automorphism-based polynomial evaluation algorithm with a computational complexity of only $O(\log d)$. However, this algorithm depends on a specific algebraic structure and can only support polynomial evaluations of limited degrees, so it is excluded here.

Algorithm	Scalar Mult.	Addition	Tensor Product	Key Switching	Modulus Switching	Multiplicative Depth
Original BSGS Algorithm	$O(d)$	$O(d)$	$\approx 3\sqrt{d}$	$\approx 2\sqrt{d}$	$\approx 2\sqrt{d}$	$\lceil\log d\rceil + 1$
Paterson-Stockmeyer Algorithm	$O(d)$	$O(d)$	$\approx \sqrt{2d}$	$\approx \sqrt{2d}$	$\approx \sqrt{2d}$	$\lceil\log d\rceil$
Asymmetric BSGS Algorithm	$O(d)$	$O(d)$	$O(\sqrt{d})$	$O(d^{1/t})$	$O(d^{1/t})$	$\lceil\log d\rceil + 1$

To keep the description concise, we ignored the influence of the constant $t$ in the asymptotic complexity of the asymmetric BSGS algorithm. However, we note that as $t$ increases, there is a factor of $t$ hidden in the complexity of key switching and modulus switching, and a factor of $2^{t - 1}$ hidden in the complexity of tensor products. Therefore, for any fixed $d$, there is a turning point at which increasing $t$ further will instead increase the overall computational cost.

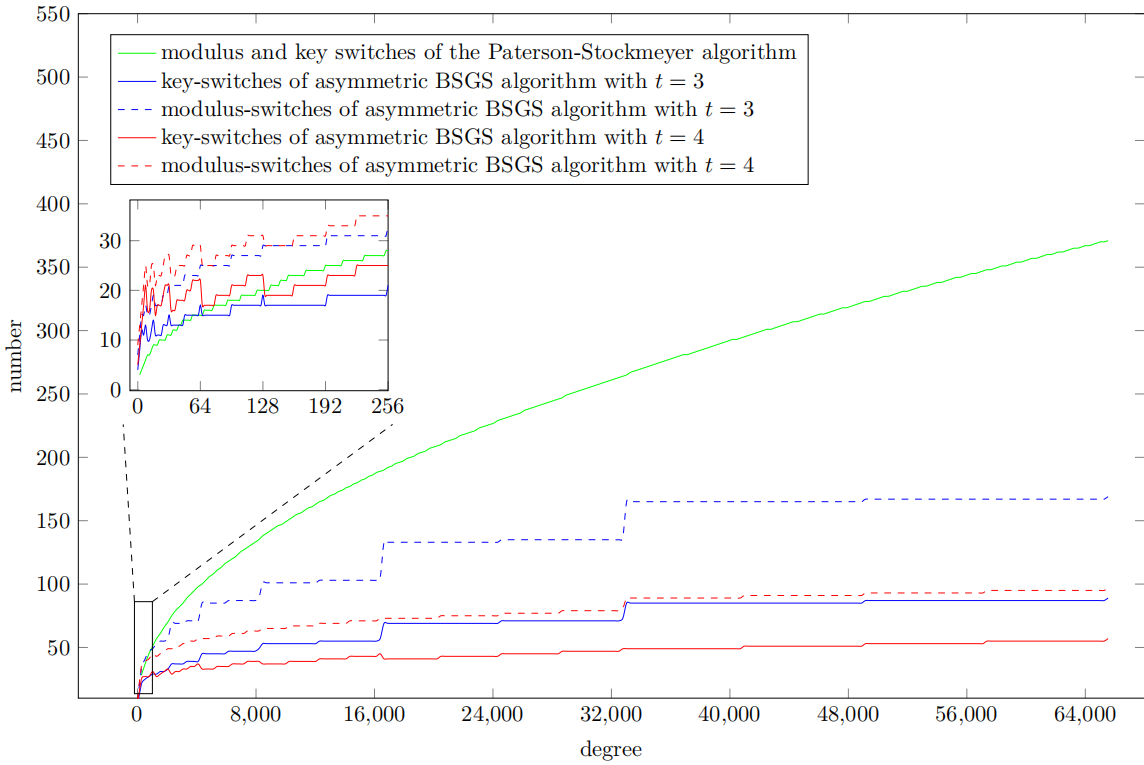
To strike a balance between the positive and negative effects, we conducted a series of experiments. The results show that for polynomials of degree less than 65536, setting $t = 4$ yields the optimal performance in most scenarios. An interesting follow-up direction would be to mitigate the negative impact of the parameter $t$ in this asymptotic complexity, so as to further increase its value.

The figure below shows the exact number of modulus switches and key switches in the asymmetric BSGS algorithm with different parameters. Although it performs worse than the Paterson-Stockmeyer algorithm for polynomials of low degrees, as the degree of the polynomial increases, the number of modulus and key switches is only a fraction of that in the Paterson-Stockmeyer algorithm.

4. Applications

The asymmetric BSGS algorithm is universal and can handle the evaluation tasks of polynomials of any degree in all leveled FHEs.

All homomorphic computing tasks that rely on high-degree dense polynomial evaluation will benefit from this, including leveled FHE bootstrapping and LWE amortized bootstrapping. For example, we obtain the following accelerations:

$2.9\times$ improvement in throughput for the bootstrapping of BGV presented in paper⁴.
$3.5\times$ decrease in latency for a recent amortized bootstrapping for LWE ciphertext presented in paper⁵.

5. References

Mike Paterson, Larry J. Stockmeyer. On the number of nonscalar multiplications necessary to evaluate polynomials. SIAM J. Comput. 1973. ↩ ↩²
Jacob Alperin-Sheriff and Chris Peikert. Practical Bootstrapping in Quasi-linear Time. CRYPTO 2013. ↩
Hiroki Okada, Rachel Player, Simon Pohmann. Homomorphic Polynomial Evaluation Using Galois Structure and Applications to BFV Bootstrapping. ASIACRYPT 2023. ↩
Shai Halevi, Victor Shoup. Bootstrapping for HElib. EUROCRYPT 2015. ↩
Zeyu Liu, Yunhao Wang. Amortized Functional Bootstrapping in Less than 7 ms, with Õ(1) Polynomial Multiplications. ASIACRYPT 2023. ↩

Algorithm	Scalar Mult.	Addition	Tensor Product	Key Switching	Modulus Switching	Multiplicative Depth
Original BSGS Algorithm	\(O(d)\)	\(O(d)\)	\(\approx 3\sqrt{d}\)	\(\approx 2\sqrt{d}\)	\(\approx 2\sqrt{d}\)	\(\lceil\log d\rceil + 1\)
Paterson-Stockmeyer Algorithm	\(O(d)\)	\(O(d)\)	\(\approx \sqrt{2d}\)	\(\approx \sqrt{2d}\)	\(\approx \sqrt{2d}\)	\(\lceil\log d\rceil\)
Asymmetric BSGS Algorithm	\(O(d)\)	\(O(d)\)	\(O(\sqrt{d})\)	\(O(d^{1/t})\)	\(O(d^{1/t})\)	\(\lceil\log d\rceil + 1\)